Definiție 7. Dacă ecuația (8.1) este îndeplinită numai pentru toți, atunci vectorii a1. a2. sunt liniar independente.
Definiția 8. Dacă se menține egalitatea, atunci spunem că vectorul b este o combinație liniară a vectorilor a1. a2. ak. sau este exprimată liniar prin acești vectori.
Rețineți că dacă vectorii a1. a2. ak sunt dependenți liniar, atunci cel puțin unul dintre vectori poate fi exprimat liniar în termenii celorlalți. Acest lucru rezultă din însăși definiția 6, deoarece, dacă cel puțin una dintre ele, atunci este posibilă realizarea împărțirii celorlalți, și atunci vom avea unde. Converse este de asemenea adevărat că, dacă unul dintre vectori este exprimat liniar în termenii celorlalți, atunci toți acești vectori sunt în mod colectiv liniar dependenți.
Rețineți că dacă vectorii a și b nu sunt coliniari sau a. b și c nu sunt coplanare. atunci acești vectori sunt liniar independenți în plan sau în spațiu, respectiv.
Arătăm acest lucru prin exemplul a trei vectori non-coplanari a. b și c. Realizăm dovada prin contradicție, presupunând că acești vectori, deși nu sunt coplanari. dar sunt dependente liniar. Apoi trebuie să fie îndeplinită dependența liniară a vectorilor, adică și lăsați-o să fie. Apoi putem împărți partea stângă și cea dreaptă a ecuației și, ca rezultat, vom avea o expresie care contrazice definiția lui 10 (""), adică deși vectorii a. b și c nu sunt coplanare. dar vectorul a este exprimat liniar în termeni de alte două b și c. ceea ce înseamnă (prin definiția 8) că acestea sunt dependente liniar. Din aceasta rezultă că vectorul a trebuie să fie liniar independent cu vectorii b și c. Este interesant faptul că într-un spațiu tridimensional orice patru vectori spațiali vor fi dependenți liniar.
Doi vectori nonzero a și b sunt ortogonali. dacă sunt perpendiculare (proiecția vectorului a pe b și proiecția vectorului b pe a sunt zero). Apoi scrieți. Astfel de vectori sunt întotdeauna independenți liniar.
Dacă vectorii nonzero a. b și c sunt perechi ortogonale, apoi formează un triple de vectori liniar independenți.
Definiția 9. Rangul unui sistem de vectori este numărul maxim de vectori liniar independenți.
Definiția 10. Un spațiu liniar este numit n-dimensional. dacă în acesta se găsesc n vectori independenți liniar și fiecare sistem format din mai mulți vectori depinde liniar în acest spațiu.
De exemplu, vectorii situați pe o singură linie. formează un spațiu unidimensional. în care există un singur vector independent. și toate celelalte pot fi exprimate prin relații lineare prin ea. Pe plan, setul de vectori formează un spațiu bidimensional. și anume în acest spațiu sunt definiți doar doi vectori independenți.
Definiție 11. Dacă un spațiu are un set finit de vectori liniar independenți, atunci el este numit vector cu dimensiuni finite. și dacă este posibil să găsim în ea în mod arbitrar mulți vectori independenți liniar în ea, atunci este infinit dimensional.
Definiția 12. Colectarea de n vectori unici liniar independenți ai unui spațiu n-dimensional se numește baza spațială n-dimensională.
Observăm că orice alte vectori definiți într-o anumită bază pot fi exprimate în termeni de vectori de bază.
Teorema. Fiecare vector x al unui spațiu linear n-dimensional poate fi reprezentat și într-un mod unic, sub forma unei combinații liniare de vectori de bază.
Dovada teoremei constă în două părți. Mai întâi demonstrăm posibilitatea de a exprima un vector arbitrar pe baza unui spațiu liniar. și apoi că descompunerea unui vector arbitrar față de o anumită bază este unică.
Fie o bază arbitrară a unui spațiu n-dimensional R și un vector arbitrar. Deoarece fiecare vector n + 1 al unui spațiu n-dimensional R este dependent de liniaritate (definiția 6), sistemul format de vectorii ll. l2. ln și x trebuie să fie dependente liniar. Aceasta înseamnă egalitatea
unde - numerele nu sunt simultan egale cu zero. Este clar că, în caz contrar, cel puțin unul dintre numere nu ar fi egal cu zero și atunci egalitatea (8.2) ar avea forma
care, la rândul său. ar arăta o dependență liniară a vectorilor de bază. Exprimăm x din (8.2), împărțind prin coeficienții lui li și transferându-le în partea dreaptă. După efectuarea transformărilor de mai sus, avem
Acum demonstrăm că extinderea (8.4) a vectorului x în raport cu baza dată l1. l2. În singurul. Să presupunem că vectorul x în spațiul R are două extensii distincte
Apoi scădem cealaltă de la o egalitate și din moment ce același vector se află pe partea stângă a egalității. atunci ajungem
în consecință, avem sistemul
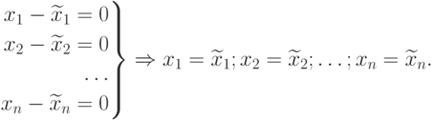
Ultima expresie demonstrează complet teorema.