Fibonacci geometrie este o secțiune de aur
Orice segment poate fi împărțit astfel încât raportul dintre părțile sale mai mici și cele mai mari să fie egal cu raportul dintre partea mai mare și segmentul întreg (fig.3-3). Acest raport este întotdeauna 0.618.
Secțiunea de aur se găsește pretutindeni în natură. Într-adevăr, corpul uman este întruchiparea Secțiunii de Aur (a se vedea figura 3-9) în tot, de la dimensiuni externe la dispozitivul feței. „Platon, în svoihTimaeus (Timeu, filosofia naturală *)“, - spune Peter Tompkins (Peter Tompkins), - „merge atât de departe încât să ia în considerare phi, iar rezultatul și raportul de aur, ca cea mai mare generalizarea relațiilor matematice și consideră că este cheia la fizica cosmosului. " În secolul al XVI-lea, Johannes Kepler (Johannes Kepler), ceea ce face note despre Golden sau „secțiunea divină“, a spus că este, de fapt, caracterizează tot în lume și, în special, simbolizează creația lumii „asemănarea“ lui Dumnezeu. O persoană împarte în centură cu raportul Fibonacci. Media este de aproximativ 0,618. Acest raport rămâne valabil separat pentru bărbați și femei separat, un semn excelent de a crea "în asemănare". Este totul în dezvoltarea omenirii și o creație "în asemănare"?
Comerțăm pe termenii cei mai favorabili. Încearcă-l gratuit!
Părțile laterale ale dreptunghiului de aur sunt în proporție 1.618k 1. Pentru a construi un dreptunghi de aur, începe cu un pătrat cu laturile unității B2 și trage o linie de la mijlocul uneia dintre laturile sale unul dintre colțuri, la partea opusă, așa cum se arată în ris.3-4.
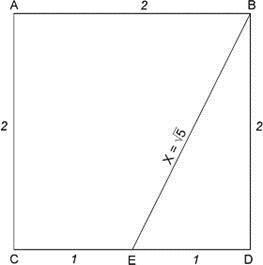
Triunghiul EDB este dreptunghiular. Pitagora, aproximativ 550 î.Hr. a dovedit că pătratul ipotentului unui triunghi drept este egal cu suma pătratelor picioarelor. În acest caz, prin urmare, X2 = 22 + 12, sau X2 = 5. Lungimea ipotenuzei este egal cu EB, atunci rădăcina pătrată 5. Următorul pas în construirea unui dreptunghi de aur este de a continua linia CD la punctul G, astfel încât EG este egală cu rădăcina pătrată a 5 sau 2.236 unități de lungime, așa cum se arată în figura 3-5. După finalizarea construcției, laturile dreptunghiului vor fi legate ca raportul de aur atât de dreptunghi și AFGC și BFGD de Aur dreptunghiuri.
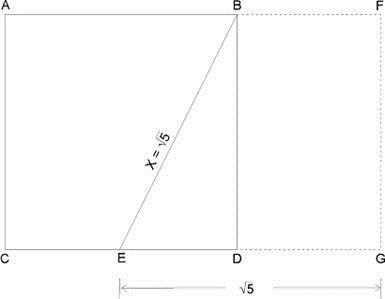
Deoarece laturile dreptunghiurilor sunt în raportul Proporția de Aur, dreptunghiurile în sine sunt, prin definiție, Dreptunghiurile de Aur.
Lucrările în artă sunt mult îmbunătățite prin cunoașterea dreptunghiului de aur. Apelul valorii și utilizării sale a fost deosebit de puternic în Egiptul antic și în Grecia și în timpul Renașterii, în toate perioadele importante de civilizație. Leonardo da Vinci (Leonardo da Vinci) acordă o importanță deosebită raportului de aur. De asemenea, el a găsit-o plăcută în relațiile sale și a spus: "Dacă obiectul nu are forma corectă, nu funcționează". Multe dintre picturile sale au aspectul potrivit, deoarece a folosit Secțiunea de Aur pentru a-și spori atractivitatea.
Deși proporția de fi fost utilizată conștient și gândită de artiști și arhitecți din motive proprii, ea are în mod evident un impact asupra observatorilor acestor forme. Experimentatorii au stabilit că oamenii găsesc raportul 0.618 estetic plăcut. De exemplu, oamenii au fost rugați să aleagă un dreptunghi dintr-un grup de dreptunghiuri de diferite tipuri, iar alegerea de mijloc era aproape de forma dreptunghiului de aur. Când li se cere să traverseze o bandă de alta așa cum le place cel mai bine, oamenii practic au folosit o bandă pentru a diviza cealaltă în raportul fi. Ferestrele, ramele de tablouri, clădirile, cărțile și crucile de cimitir corespund adesea aproximativ dreptunghiului de aur.
La fel ca Secțiunea de Aur, valoarea Dreptunghiului de Aur este aproape limitată la frumusețe, dar servește și această activitate. Printre numeroasele exemple, cea mai izbitoare este faptul că dublul helix al ADN-ului însuși creează o secțiune aurie în intervalele standard ale curbelor sale (vezi figura 3-9).
În timp ce raportul de aur și de aur dreptunghi reprezintă forme statice de o frumusețe naturală și crearea și activitatea omului, performanta dinamism estetic placut, organizat de creșterea și dezvoltarea mișcării poate fi realizată numai forma cea mai perfectă din univers - spirala de aur.
Un dreptunghi de aur poate fi folosit pentru a construi spirala de aur. Orice dreptunghi de aur, ca în figura 3-5, poate fi împărțit într-un pătrat și într-un dreptunghi de Aur mai mic, așa cum se arată în figura 3-6. Acest proces poate continua teoretic pe o perioadă nedeterminată. Aceste dreptunghiuri rezultate, pe care le-am desenat și care, așa cum sa dovedit, sunt curbate spre interior, sunt etichetate A, B, C, D, E, F și G.
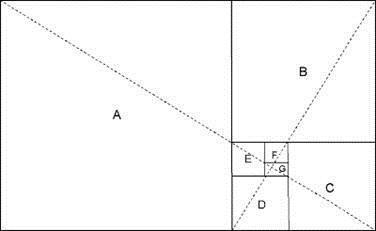
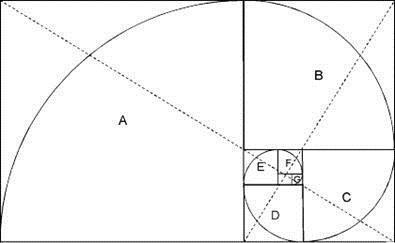
Liniile dotate, care sunt ele însele în raport de aur, disecă dreptunghiurile în diagonală și cu precizie în centrul teoretic al pătratelor răsucite. Aproximativ de la punctul central, putem trage o spirală, așa cum se arată în figura 3-7, care leagă punctele de intersecție ale fiecărui pătrat de răsucire în ordinea dimensiunilor în creștere. Deoarece patratele sunt curbate spre interior și spre exterior, punctele lor de legătură scriu spirala de aur. Pentru construirea spiralei de aur, același proces poate fi folosit, dar cu utilizarea triunghiurilor de răsucire.
În orice moment al dezvoltării Helixului de Aur, raportul dintre lungimea arcului și diametrul său este de 1.618. Diametrul și raza, la rândul său, corelează cu diametrul și raza, distanțate la un unghi de 90 °, cu un coeficient de 1,618, așa cum se arată în figura 3-8.
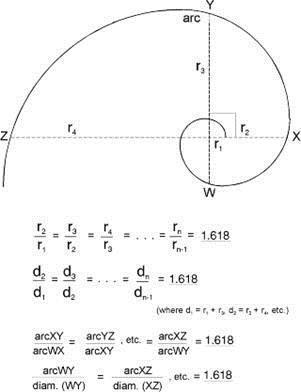
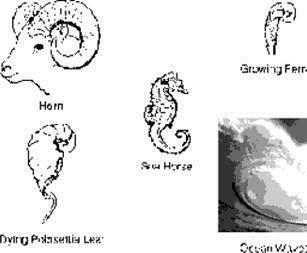
Spirala de aur, care este un fel de spirală logaritmică sau izogonală, nu are limite și este constantă în formă. Din orice punct al spiralei, vă puteți mișca fără sfârșit fie în interior, fie în afară. Partea centrală a spiralei logaritmice, privită printr-un microscop, ar avea același aspect ca cea mai largă parte vizibilă a acesteia, la o distanță de mulți ani lumină. Așa cum a subliniat David Bergamini (David Bergamini) în matematică, coada cometei este derulată de soare în formă de spirală logaritmică. Spiderul Epeira își învârte pânza în formă de spirală logaritmică. Bacteriile se înmulțesc într-o progresie logaritmică, care poate fi trasă ca o spirală logaritmică. Meteoritii, coborâți în suprafața Pământului, formează cavități care se corelează cu o spirală logaritmică. conuri de pin, Seahorse, cochilii de melci, scoici de moluste, valurile oceanului, ferigi, coarne de animale și dispunerea semințelor de floarea-soarelui și margaritki- ele formează o spirală logaritmică.
Nori ai unui ciclon și a unor galaxii ale unui spațiu deschis sunt răsucite în spirale logaritmice. Chiar și degetul uman, care este compus din trei falange situate în raport cu celălalt în raportul de aur, are o formă elicoidală pe moarte foaie când este comprimat. În figurile 3-9 vedem reflectarea acestei influențe cosmice în numeroase forme. Veșnicia de timp și ani lumină de spațiu comun de un con de pin și o galaxie spirală, dar structura rămâne aceeași: coeficientul de 1.618, eventual imperative legea care reglementează activitatea fenomenelor naturale. Astfel, spirala de aur se desfășoară în fața noastră în formă simbolică, ca fiind unul dintre natura maiestuoasa a planurilor, viața în expansiune infinită și contracția, o lege statică care reglementează un proces dinamic, susținut de interiorul și în afara proporției de 1.618. Secțiunea de aur.