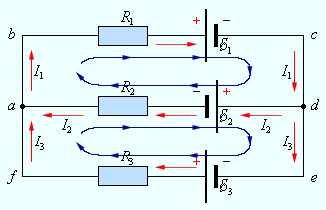
Fig. 4.24. Un exemplu de circuit electric ramificat.
Lanțul conține un nod independent (a sau d) și două bucle independente (de exemplu, abcd și adef)
Normele lui Kirchhoff permit determinarea puterii și a direcției curentului în orice parte a circuitului ramificat dacă sunt cunoscute rezistențele secțiunilor sale și ale EMF incluse în ele. Numărul de ecuații compilate în conformitate cu prima și a doua reguli Kirchhoff trebuie să fie egal cu numărul de cantități necunoscute. Folosind prima regulă Kirchhoff pentru un lanț ramificat care conține node m și ramuri (secțiuni) se pot scrie (m - 1) ecuații independente și se utilizează ecuația independentă (n - m + 1).
Să dăm un exemplu de calcul al curenților într-un circuit cu ramificație (Figura 4.25).
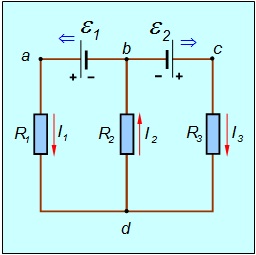
Fig. 4.25. Exemplu de lanț ramificat
Direcțiile acțiunii EMF sunt arătate de săgețile albastre. În acest lanț, avem două noduri - punctele b și d (m = 2) și trei ramuri - secțiunea b - a - d cu curentul I1. secțiunea b -d cu curentul I2 și secțiunea b -c -d cu curentul I3 (n = 3). Prin urmare, putem scrie o ecuație (m - 1 = 2 - 1 = 1) bazată pe prima regulă Kirchhoff și pe două ecuații (n - m + 1 = 3 - 2 + 1 = 2). Cum se face acest lucru în practică?
Pasul unu. Alegem direcțiile curenților care curg în fiecare ramură a lanțului. Cum de a alege aceste direcții este absolut neimportantă. Dacă am ghicit, în rezultatul final valoarea acestui curent va deveni pozitivă, dacă nu, iar direcția ar trebui să fie contrariul - valoarea acestui curent se va dovedi a fi negativă. În exemplul nostru, am ales direcția curenților așa cum se arată în figură. Este important să subliniem că direcțiile EMF nu sunt arbitrare, ele sunt determinate de metoda de conectare a polilor surselor curente (a se vedea Figura 4.25).
Pasul doi. Vom scrie prima regulă Kirchhoff pentru toate nodurile, cu excepția unuia (în ultimul nod, ale cărui alegere este arbitrară, această regulă va fi executată automat). În cazul nostru, putem scrie ecuația pentru nodul b. care include curentul I2 și curenții I1 și I3
Pasul trei. Rămâne pentru noi să scriem ecuațiile (în cazul nostru, două) pentru a doua regulă Kirchhoff. Pentru aceasta, trebuie selectate două circuite închise independente. În exemplul examinat, există trei astfel de posibilități: calea de-a lungul conturului din stânga b -a -d -b. calea de-a lungul conturului din dreapta b -c -d -b și traseul în jurul întregului lanț b -a -d -c -b. Este suficient să luați două dintre ele, iar pentru al treilea contur, regula a doua Kirchhoff va fi executată automat. Direcția de traversare a conturului rolului nu joacă un rol, dar curentul va fi luat cu un semn plus dacă acesta curge în direcția trecerii și cu un semn minus dacă curentul curge în direcția opusă. Același lucru este valabil și pentru semnele EMF.
Luați conturul b -a -d -b pentru a începe. Ieșim punctul b și ne mișcăm în sens invers acelor de ceasornic. În drumul nostru vor exista două curenți, I1 și I2. direcțiile care coincid cu direcția aleasă de ocolire. De asemenea, EMF acționează în aceeași direcție. Prin urmare, a doua regulă Kirchhoff pentru această parte a lanțului este scrisă ca
Ca a doua cale închisă pentru o varietate, alegem calea b -a -d -c -b în jurul întregului lanț. În acest fel întâlnim două curente I1 și I3. dintre care primul va intra cu un semn plus, iar al doilea - cu un semn minus. Ne vom întâlni, de asemenea, cu două EMF-uri, din care va intra în ecuațiile cu un semn plus și - cu un semn minus. Ecuația pentru această cale închisă are forma
Ultima valoare a fost negativă pentru caracteristicile numerice date ale lanțului. Prin urmare, în realitate direcția curentului este inversată așa cum se arată în figură. Acest lucru este natural: o sursă stângă puternică trimite un curent de 0,75 A, o parte din care (0,45 A) ramificații în ramura mijlocie, iar restul - 0,3 A - continuă să curgă în aceeași direcție, ceea ce nu poate fi împiedicat de o baterie de putere redusă.
Notă. Normele lui Kirchhoff permit, în principiu, calcularea unor lanțuri complexe arbitrar. Dar calculele pot fi destul de complicate. Prin urmare, este recomandat să căutați mai întâi posibila simetrie a lanțului. Uneori, din considerente de simetrie, este mai mult sau mai puțin evident că unii curenți sunt egali unul cu celălalt sau anumite tensiuni sunt zero (iar apoi această secțiune a lanțului poate fi exclusă din considerare). Dacă acest lucru este posibil, calculele sunt mult simplificate.
În exemplul nostru, am neglijat rezistența internă a surselor curente. Dacă sunt prezenți, trebuie să fie incluse și în ecuațiile celei de-a doua reguli a lui Kirchhoff.
Un exemplu. Două surse de curent identice cu EMF și rezistența internă r sunt conectate la baterie. Există două conexiuni posibile - serial și paralel (Figura 4.26). La ce legătură va fi curentul din sarcina R cel mai mare?
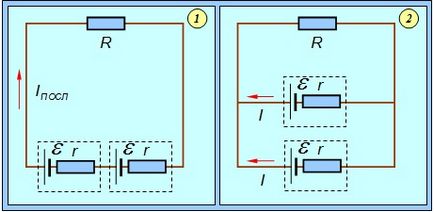
Fig. 4.26. Serial (1) și paralel (2) de conectare a surselor de alimentare
Soluția. Calculul este foarte simplu pentru o conexiune serială: ecuația primei reguli a lui Kirchhoff lipsește, deoarece nu există noduri în lanț. Singura ecuație din a doua lege oferă
Pentru a simplifica calculul unei conexiuni paralele, avem în vedere că din considerente de simetrie, curenții prin surse trebuie să fie egali și să coincidă în direcție. Apoi este dată prima regulă Kirchhoff