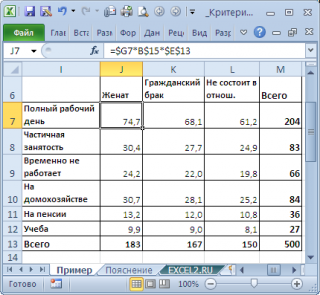
Să presupunem că avem un eșantion de date care reprezintă rezultatul unui sondaj de 500 de persoane. Oamenii a fost stabilit 2 întrebări: despre statutul lor marital (căsătorit, uniune civilă, nu se află într-o relație) și nivelul lor de ocupare (full-time, part-time, temporar, nu lucrează la gospodărie, la pensie, studiind). Toate răspunsurile au fost plasate în tabel:
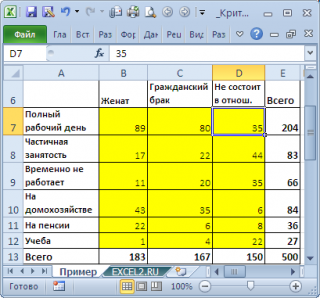
Acest tabel este numit tabel de situație de urgență (sau tabel de factori, tabel de contingență în limba engleză). Elementele de la intersecția rândurilor și coloanelor din tabel sunt, de obicei, denominate Oij (din frecvențele actuale observate în engleză, adică observate).
Suntem interesați de întrebarea "Situația civilă afectează ocuparea forței de muncă?", Adică există o relație între cele două metode de clasificare a eșantionului?
Atunci când testează ipoteze de acest tip, se presupune de obicei că ipoteza nulă afirmă că nu există nici o dependență de metodele de clasificare.
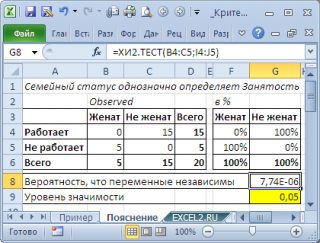
În acest caz, starea civilă determină în mod unic angajarea (vezi exemplul fișei explicative). În schimb, un alt exemplu al independenței este un alt rezultat al sondajului:
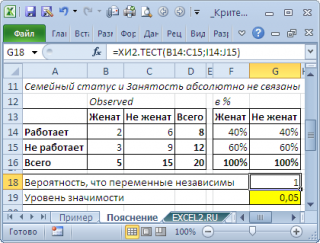
Vă rugăm să rețineți că procentul de angajare în acest caz nu depinde de starea civilă (aceeași pentru femeile căsătorite și necăsătorite). Aceasta coincide cu formularea ipotezei nul. Dacă ipoteza nulă este adevărată, atunci rezultatele sondajului ar trebui să fie distribuite în tabel astfel încât procentul celor angajați să fie același indiferent de starea civilă. Folosind acest lucru, vom calcula rezultatele sondajului care corespund ipotezei nula (a se vedea exemplul fișierului exemplu).
În primul rând, vom calcula probabilitatea estimării că un element eșantion va avea o anumită ocupare a forței de muncă (a se vedea coloana ui):
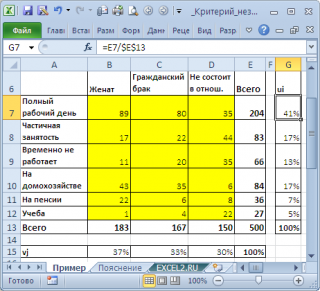
unde c este numărul de coloane (coloane) egal cu numărul de niveluri ale variabilei "Starea civilă".
Apoi se calculează probabilitatea estimării că elementul de eșantionare va avea o anumită stare maritală (a se vedea linia vj).
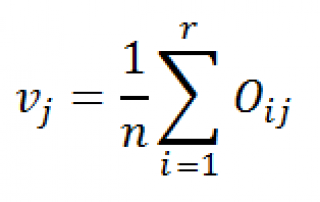
unde r este numărul de rânduri (rânduri) egal cu numărul de niveluri ale variabilei "Ocuparea forței de muncă".
Frecvența teoretică pentru fiecare celulă Eij (din limba engleză așteptată, adică frecvența așteptată) în cazul independenței variabilelor este calculată prin formula:
Eij = n * ui * vj
Se știe că statistica X 2 0 pentru n-ul mare are aproximativ o distribuție CI2 cu grade (r-1) (c-1) de libertate (df-grade de libertate):
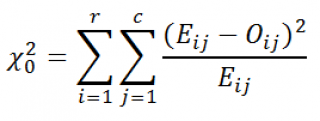
Notă. Statisticile de mai sus pentru c = 1 este utilizată pentru a calcula consens Pearson testul chi-pătrat (a se vedea. Articolul Ipoteză Testarea chi-pătrat Pearson MS Excel).
Dacă valoarea acestei statistici este "prea mare" (mai mare decât valoarea pragului), atunci ipoteza nulă este respinsă. Valoarea pragului este calculată pe baza nivelului de semnificație. de exemplu, folosind formula = ХІ2.
Notă. Nivelul de semnificație este de obicei considerat a fi 0,1; 0,05; 0.01.
Când se testează ipoteza, este de asemenea convenabil să se calculeze valoarea p. pe care o comparăm cu nivelul de semnificație. Valoarea p se calculează folosind distribuția CI2 cu (r-1) * (c-1) = df grade de libertate.
Dacă probabilitatea ca o variabilă aleatoare având o distribuție CI2 cu grade de libertate (r-1) (c-1) să ia o valoare mai mare decât statistica calculată X 2 0, P (r-1) * (c-1)> X 2 0> este mai mică decât nivelul de semnificație. atunci ipoteza nulă este respinsă.
În MS EXCEL, valoarea p poate fi calculată folosind formula = ХИ2. desigur, calculând imediat înainte de aceasta valoarea statisticilor X 2 0 (acest lucru se face în fișierul exemplu). Cu toate acestea, este mai convenabil să utilizați funcția HI.TEST (). Ca argumente ale acestei funcții sunt indicate referințele la intervale care conțin frecvențele teoretice (Observate) și cele calculate (așteptate) calculate.
Dacă nivelul de semnificație> valori p. atunci aceasta înseamnă frecvențele reale și teoretice calculate din ipoteza valabilității ipotezei nul. diferă serios. Prin urmare, ipoteza nulă trebuie respinsă.
Utilizarea funcției HI2.TEST () vă permite să accelerați procedura de testare a ipotezelor. deoarece nu este necesar să se calculeze valoarea statisticilor. Acum este suficient să comparăm rezultatul funcției CH.TEST () cu un anumit nivel de semnificație.