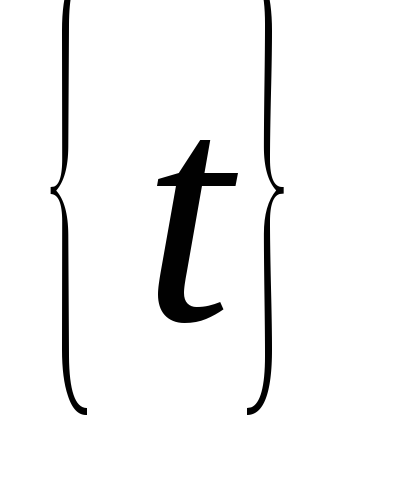
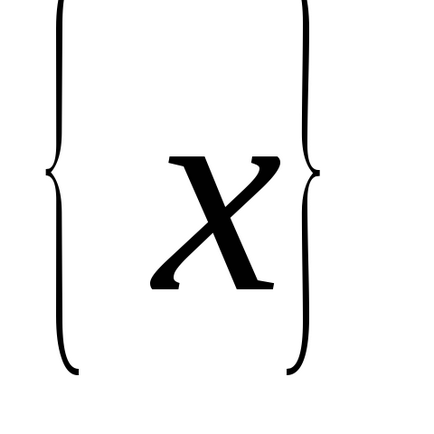
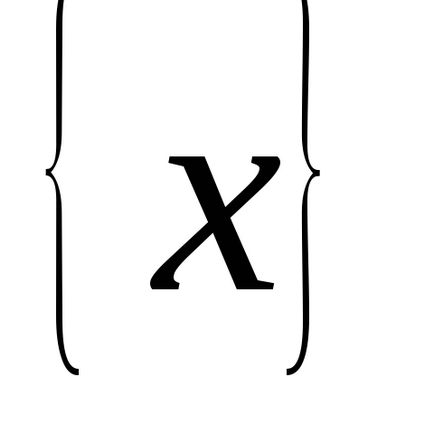
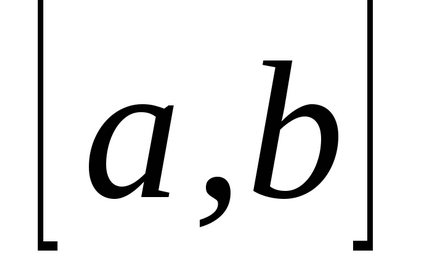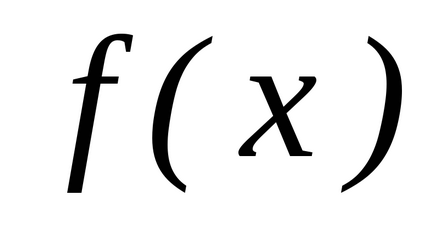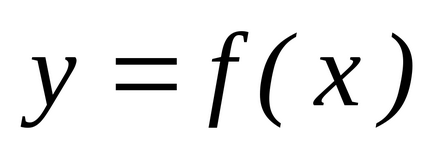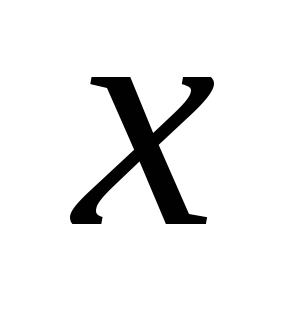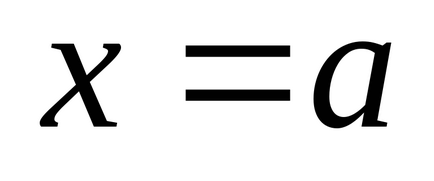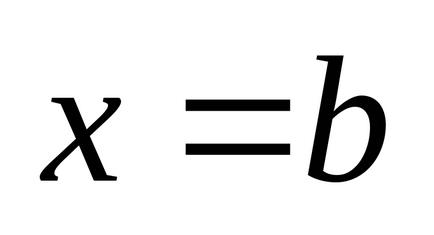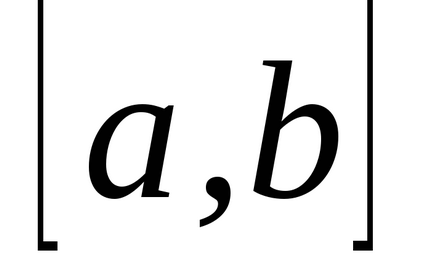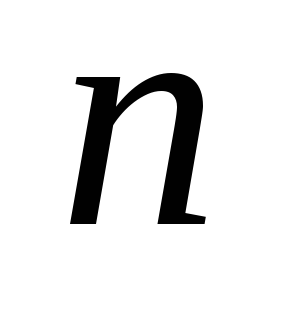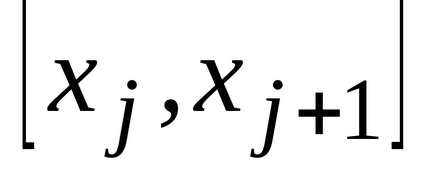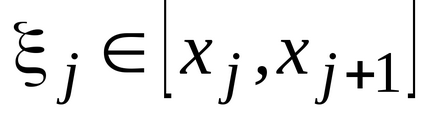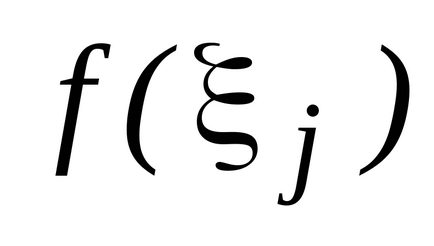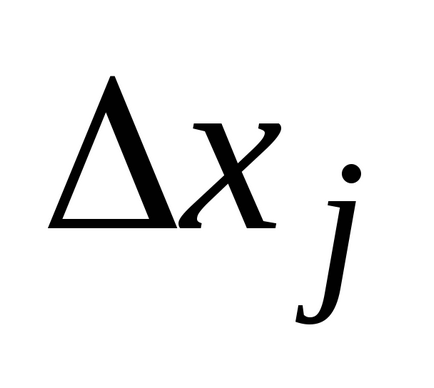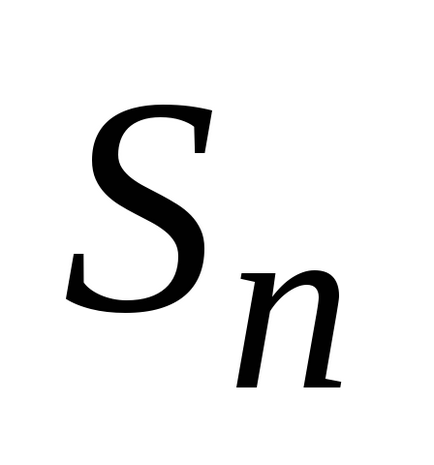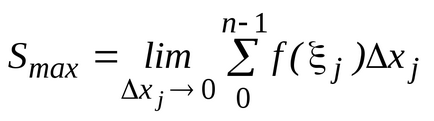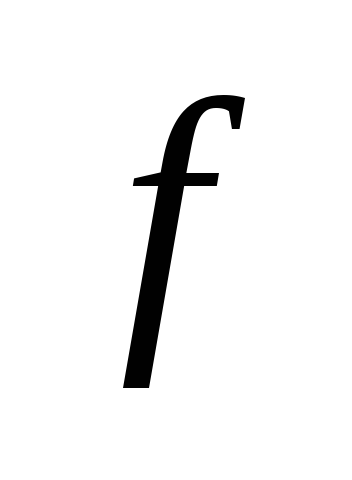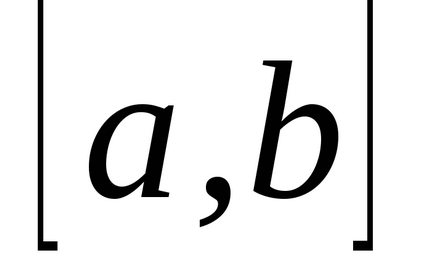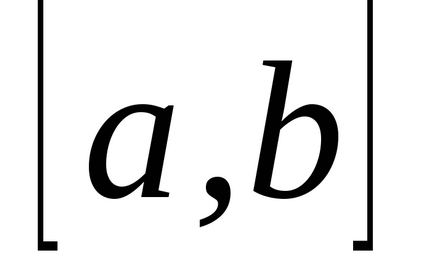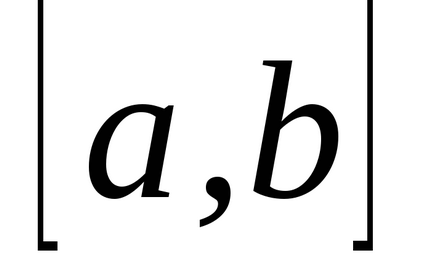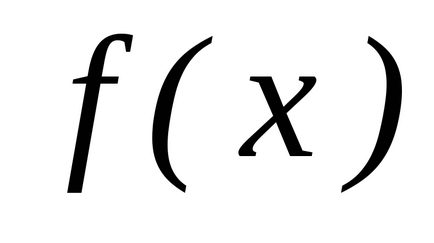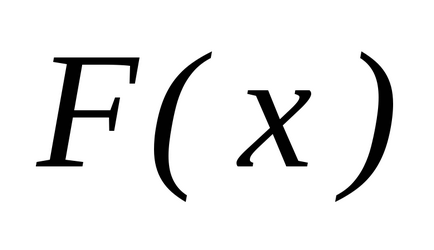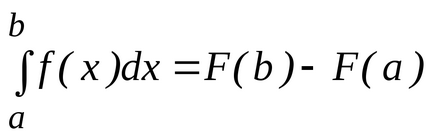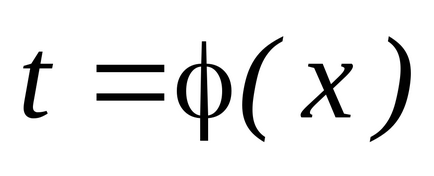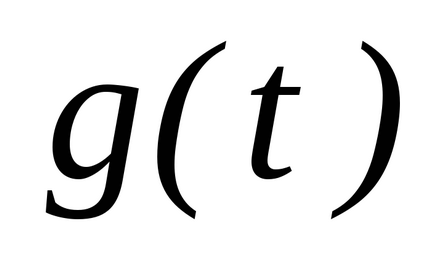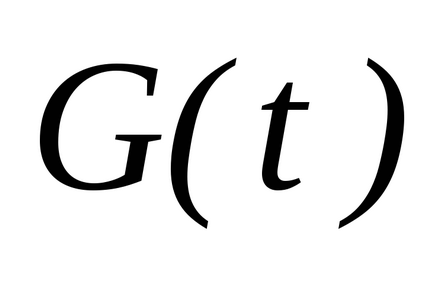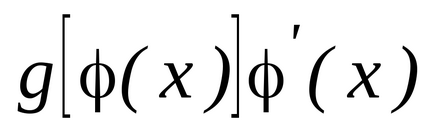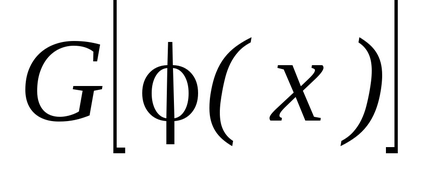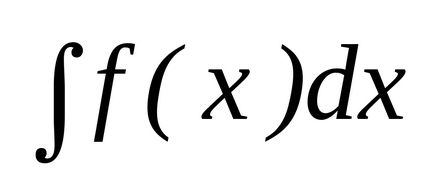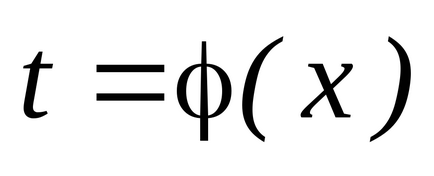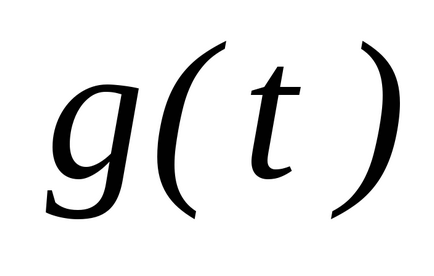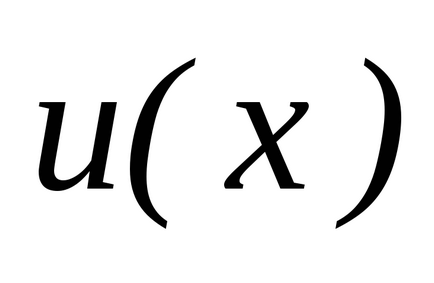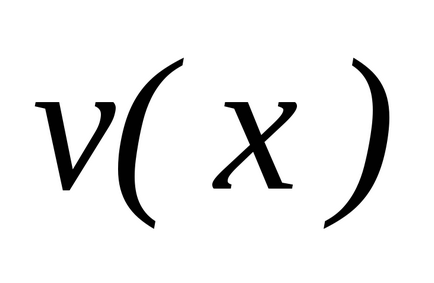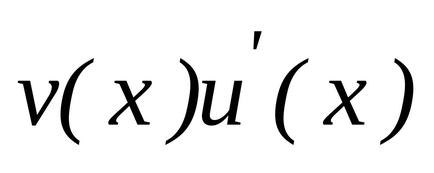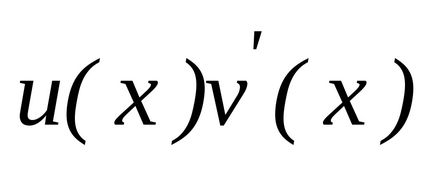Am stabilit intervalul
(a și b sunt numere finite) o funcție continuă non-negativă. Îi prezentăm graficul și definim conceptul de zonă a unei figuri delimitată de o curbă, axă, directșiși calculați această zonă. Împărțim segmentulpepărți pe puncte, pe fiecare dintre segmentele obținute(j = 0, 1, ..., n-1) într-un punct arbitrardefiniți valorilefuncționează la aceste puncte și alcătui suma: care se numește suma integrală și care este egală cu suma zonelor de dreptunghi. Acum ne vom strădui pentru tot la zero și astfel încât tăierea parțială maximă (cea mai mare) a descompunerii tinde la zero. Dacă în acest caz cantitateasă depună eforturi pentru o anumită limită, independent de metodele de împărțire și selecție a punctelor. Atunci cantitateasă o numim zonă a figurii noastre curbe. T .:.:.
Distrazându-ne de operarea găsirii zonei, vom considera această operație ca găsind un anumit număr
pentru această funcție, dată pe interval:.
Un integral integrat al funcției pe interval
Limita sumei integrale este numită atunci când segmentul parțial maxim al partiției tinde la zero.
Să i se acorde o funcție continuă
funcțieși lăsațiexistă primitivul său. Teorema lui Newton-Leibniz afirmă validitatea următoarei egalități:.
Metode de bază pentru integrare
Integrarea prin substituție a unei variabile (substituție)
Lăsați funcția
este definită și diferențiată pe un anumit set, și lăsațiset de toate valorile acestei funcții. Să presupunem în plus că pentru funcția respectivăexistă pe setfuncție antiderivativă, și apoi peste tot pe scenăpentru funcția respectivăexistă o funcție antiderivativă egală cu, care este,
.
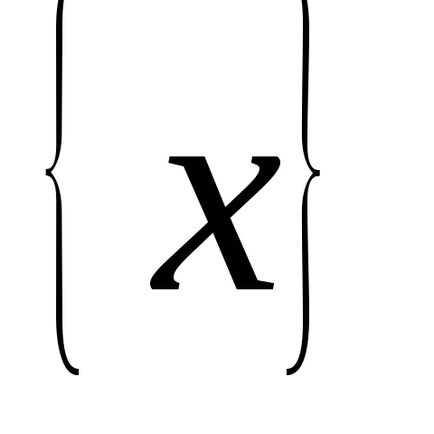
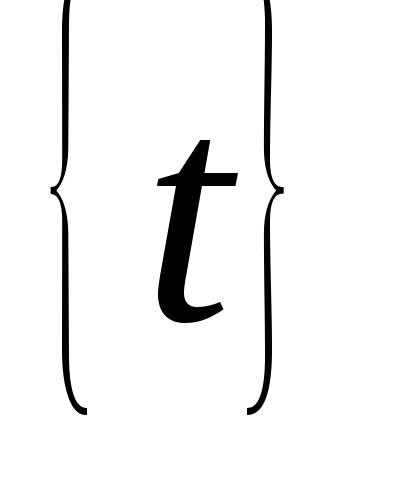
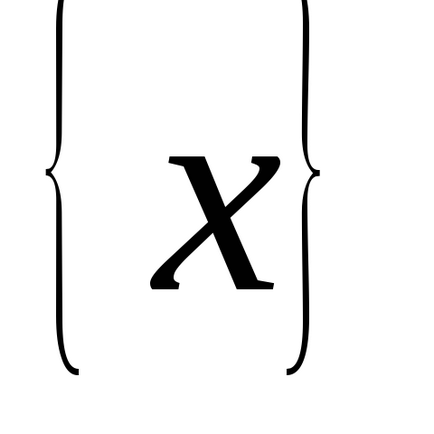
Trebuie să calculam integral
și puteți selecta o funcție ca variabilă nouăastfel încât, cuușor de integrat, adică:
și - această metodă de calcul se numește integrare prin schimbarea unei variabile.
Integrarea pe părți
Lăsați fiecare dintre funcții
șieste diferențiat pe setși, în plus, pe acest set există un antiderivativ pentru funcție. Apoi, pe setexistă o funcție antiderivantă pentru această funcție, și formula
.
Articole similare