14 Secvențe funcționale și serii
Până în prezent am considerat numai secvențe numerice și serii numerice. Acum vom studia secvențele ale căror elemente sunt funcții și, de asemenea, seria a cărei summands sunt funcții.
14.1 Convergența punctuală și uniformă
Luați în considerare o serie de funcții
f1 (x). f2 (x). f3 (x). definită pe setul E / R. Luați orice. Înlocuind un loc în loc de x. obținem o secvență numerică n (a)>. Poate converge, dar poate fi și diferită. Setul de numere a. cu substituția căruia obținem o secvență numerică convergentă, se numește domeniul convergenței secvenței n (x). Denumim acest set prin litera D:
Pentru fiecare aÎD există o limită finită, pe care o denotăm prin f (a):
.
Am folosit notația funcțională f (a) atunci când indicăm un număr pentru a accentua: această limită depinde de a. și anume aceasta este o funcție a. Puteți utiliza notația mai familiară pentru o variabilă:
, fără să uităm că f (x) este definită numai pe setul D. De asemenea, folosim o înregistrare fără simbolul lim. . O astfel de convergență a secvenței n (x)> la o funcție f (x) se numește punctual. Oferim o definiție a convergenței punctuale în limba "e-d":
.
Acum, dăm o definiție a convergenței uniforme, pe care o vom denumi după cum urmează: (citește: "secvența fn (x) converge uniform pe setul D la funcția f (x)"). Prin definiție
.
La prima vedere, diferența dintre definiții este mică, dar este semnificativă. În prima definiție, este necesar ca pentru fiecare x, D să existe un număr n0 cu o anumită proprietate. Pentru x diferite, astfel de numere pot fi diferite. În a doua definiție, cerința este mai puternică: același număr n0 ar trebui să fie potrivit pentru orice xÎD. Astfel, este clar că convergența uniformă presupune o convergență punctuală:
.
Conversia nu este adevărată, a se vedea exemplul 1 de mai jos.
Să dăm o ilustrare geometrică conceptului de convergență uniformă. Cerința conținută în definiție:
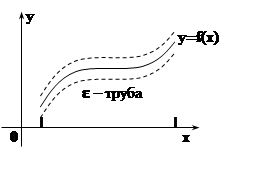
înseamnă că, începând cu un anumit număr, graficele funcțiilor fn (x) diferă foarte puțin de graficul f (x) din întregul set D. Ele se află în "e-trenul" graficului funcției f (x). Și așa,
graficele fn (x) se află în "e-tubul" graficului f (x).
Example1. Luați în considerare o serie de funcții
Presupunem că xÎD = [0, 1]. În fiecare punct al acestui set, secvența converge: