Difracția de la o gaură rotundă. Pose pe calea ecranului opac lumina val sferic cu o tăietură în acesta o gaură circulară cu raza R, astfel încât perpendiculara a scăzut de la sursa S, a lovit centrul găurii. În extensia acestei gauri luăm punctul B. Pentru R< unde m este un număr întreg, atunci gaura va lăsa exact primele zone Fresnel deschise (a se vedea formula (4)). În consecință, numărul de zone Fresnel deschise este dat de În conformitate cu formula (5), amplitudinea la punctul B: Înainte de Am, se face un semn plus, dacă m este ciudat și minus dacă m este egal. Reprezentând expresia (11) în forma (6), ajungem la relațiile: În ultima expresie, amplitudinile din zonele învecinate sunt practic aceleași. Prin urmare, Am-1/2-Am poate fi înlocuit cu - Am / 2. Atunci primim: unde semnul plus este luat pentru ciudat și minus pentru even. În funcție de numărul de perechi paralel sau paralel al zonei Fresnel este deschis la punctul B, iluminarea se va schimba. Când deschideți un număr impar de zone, veți vedea un maxim. Prin creșterea razei diafragmei sau a ecranului de compensare cu o deschidere, astfel încât să înceapă să deschidă o intensitate maximă chiar și o zonă Fresnel va scădea, iar la o valoare ajunge la un nivel minim. Iluminarea aceeași la diferite puncte ale ecranului este, de asemenea, determinată de paritatea numărului de zone Fresnel deschise, formând lumină alternantă și inele concentrice întunecate. Când mutați ecranul în paralel cu tine, aceste inele se schimbă alternativ (vezi Fig.4). Dacă gaura deschide doar o parte a primei zone, pe ecran apare un spot luminos neclare; lumina alternantă și inelele întunecate nu sunt respectate în acest caz. Dacă gaura deschide prea multe zone, alternanța inelelor luminoase și întunecate se observă numai într-o zonă foarte îngustă la limita umbrei geometrice.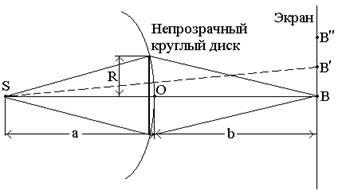
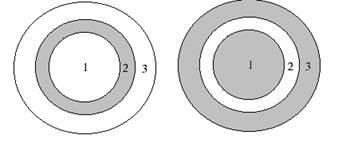
Difracția de pe un disc circular. Dacă discul circular opac cu raza R, S interpus între sursa de lumină și observarea punctului B (figura 4), m închide prima zonă Fresnel, amplitudinea la punctul B este egal cu:
Expresiile din paranteze pot fi aproximative egale cu zero. atunci
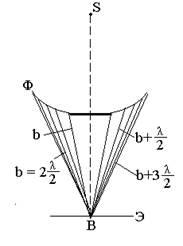
În acest caz, porțiunea de disc închisă a suprafeței undei este eliminată din considerație și zona Fresnel deschise construite după cum se arată în figură, de la marginile discului. Repetarea argumentele pentru cazul de difracție dintr-o deschidere circulară, constatăm că amplitudinea vibrațiilor rezultate excitate la punctul în toate zonele Fresnel deschise egale cu jumătate din amplitudinea datorită primei zone Fresnel deschise. În consecință, se observă întotdeauna un maxim la punctul B (un punct slab numit punct Poisson) corespunzând la jumătate din acțiunea primei zone deschise Fresnel. Cu o creștere a diametrului discului, prima zonă deschisă Fresnel este îndepărtată din punctul B și luminozitatea punctului Poisson scade. la dimensiunile mari ale discului, se observă o umbră în spatele acesteia, în apropierea căreia se observă un model de difracție foarte slab.