Astăzi, cuvântul "Integral" poate fi auzit destul de des și, adesea, în locurile cele mai neașteptate, de exemplu, pe canalul de televiziune sau pe știri. Adesea audem expresia "indicatori integrați". cuvântul "integrat", "integrativ" și altele asemenea. Ei bine, în general, oficialii și prezentatorii de televiziune, în general, se bucură foarte mult de cuvinte inteligente, deși abia înțeleg adevăratul lor sens. Și astăzi vom vorbi despre ceea ce este integrat, ce fel de integritate există și care sunt diferențele dintre ele.
Care este integralitatea
Integral este un cuvânt latin care a venit la noi din antichitate și înseamnă "întreg" sau "complet". Asta este, este clar că dacă un obiect, de exemplu, un recipient de lapte era considerat a fi un "întreg", însemna că era plin, și că în el era cât de mult lapte.
În timp, acest cuvânt a început să fie folosit în discipline complet diferite - în filosofie, politică, economie, algebră și geometrie. Dar cea mai simplă interpretare a integralului este dată de matematică.
Deci, integralul este o sumă de părți separate. Iată cele mai simple exemple pentru o înțelegere mai clară a esenței acestui termen:
- Obiectul este integrarea (sumă) a moleculelor.
- O foaie într-o celulă este o parte integrală a celulelor.
- Sistemul solar este integrat al soarelui și al planetelor.
- Societatea este integrarea oamenilor.
- Un segment este suma integrală a contoarelor. Dacă o bucată mică, apoi centimetri, milimetri sau segmente microscopice.
- Suprafața oricărei suprafețe este un ansamblu de metri pătrați, centimetri pătrați sau milimetri, precum și zone microscopice.
- Volumul este un număr integral de metri cubi sau, după cum sunt numiți și litri.
Ce este un integrat definit și nedeterminat?
Să începem cu un anumit, deoarece sensul său este mai ușor de înțeles.
Geometria studiază zona. De exemplu, dacă doriți să lipiți tapetul acasă, trebuie să știți zona de perete pentru a vedea câte imagini de fundal trebuie să le cumpărați. Apoi, înmulțiți lungimea peretelui până la înălțime și obțineți zona. În acest caz, această zonă este integrată de metri pătrați sau de centimetri, în funcție de unitățile în care ați măsurat-o. Dar suprafețele a căror zonă trebuie să le calculam departe de întotdeauna au forma unui dreptunghi, a unui pătrat sau chiar a unui cerc. În cele mai multe cazuri, acestea sunt figuri complexe cu fețe derulante. Cel mai obișnuit exemplu este domeniul figurului sub curbă având ecuația y = 1 / x. Faptul este că este imposibil să-și găsească zona cu ajutorul formulelor obișnuite prin care găsim zona unui pătrat, a unui cerc sau chiar a unei sfere. În acest scop, sa dezvoltat un integrat clar.
Esența metodei este că figura noastră complexă trebuie împărțită în dreptunghiuri foarte înguste, atât de înguste încât înălțimea fiecăruia dintre cele două adiacente este aproape egală. În mod clar, de fapt, puteți reduce infinit grosimea acestor dreptunghiuri, deci pentru a indica grosimea lor, se folosește mărimea dx. X este coordonata, iar prefixul d este desemnarea unei cantitati care scade infinit. Prin urmare, atunci când scriem dx - înseamnă că luăm un segment de-a lungul axei x. a cărui lungime este foarte mică, este practic zero.
Deci, deja am fost de acord că zona oricărei figuri este un număr integral de metri pătrați sau orice alte figuri cu zone mai mici. Apoi, figura noastră, a cărei zonă căutăm, este integrarea sau suma acestor dreptunghiuri infinit de subțiri la care l-am rupt. Și zona ei este suma zonelor lor. Adică, întreaga noastră sarcină se reduce la găsirea zonei fiecăruia dintre aceste dreptunghiuri, și apoi să le adăugăm pe toate - acesta este integralul definitiv.
Acum, să vorbim despre integritatea nedeterminată. Numai, pentru a înțelege ce este, trebuie mai întâi să știți despre derivat. Deci, să începem.
Un derivat este unghiul de înclinare a unei tangente la orice grafic într-un anumit punct al acestuia. Cu alte cuvinte, derivatul este măsura în care graficul este înclinat în locul său. De exemplu, o linie dreaptă în orice punct are aceeași panta, iar curba este diferită, dar poate fi repetată. Pentru a calcula derivatul, există formule speciale, iar procesul de calcul al acestuia se numește diferențiere. Ie Diferențierea este determinarea pantei graficului la un anumit punct.
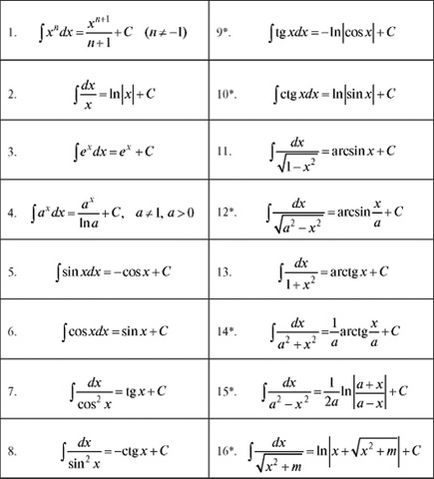
Tabelul integralelor de bază nedefinite
Și pentru a face opusul - pentru a învăța formula grafului din unghiul înclinării sale, a apela la funcționarea integrării sau la însumarea datelor despre toate punctele. Integrarea și diferențierea sunt două procese reciproce. Numai aici nu este folosită deja de integrale care a fost în primul paragraf (pentru a determina zona), ci de celălalt - nedefinit, adică fără limite.
Să presupunem că știm că derivatul unei funcții este 5. 5 este unghiul de înclinare al graficului la axa x la un anumit punct. Apoi, integrând derivatul, aflăm că funcția acestui derivat, numită și antiderivativă - y = 5x + c. unde c este orice număr. Pentru integrare, precum și pentru diferențiere, există formule speciale care pot fi găsite în tabele.
concluzie
În concluzie, vom relua faptul că principala diferență dintre un anumit integral și un termen nedeterminat este în atribuțiile lor. Anumite integrale sunt folosite pentru a calcula parametrii delimitate, cum ar fi zona, lungimea sau volumul, și cei nedefiniți atunci când se calculează parametrii care nu au limite, adică funcții.