Rădăcina puterii n a numărului a este definită [1] ca număr b. că b n = a. = a.> Aici, n este un număr natural. numit exponentul rădăcinii (sau gradul rădăcinii); ca regulă, este mai mare sau egală cu 2, deoarece cazul n = 1 este trivial.
Exemple pentru numere reale:
După cum se vede din primul exemplu, o rădăcină reală poate avea două valori (pozitive și negative), ceea ce face dificilă lucrul cu rădăcinile. Pentru a asigura neechivocitatea, se introduce conceptul de rădăcină aritmetică. a căror valoare este întotdeauna inerentă, în primul exemplu acest număr este de 3.
Definiție și concepte conexe
În plus față de cele de mai sus, putem da două definiții echivalente ale rădăcinii [2]:
- Rădăcina puterii n a a este soluția x a ecuației x n = a = a> (rețineți că pot exista mai multe soluții sau nici una)
- Rădăcina puterii n a a este rădăcina polinomului x n # x2212; a. -a,> adică, valoarea lui x. unde acest polinom este zero.
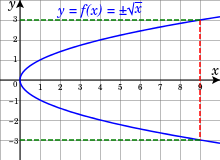
Graficul valorilor rădăcinii pătrată. la fiecare valoare a lui x. cu excepția zero, corespund două valori ale rădăcinii (y). distins printr-un semn
Funcționarea calculării unui n] >> se numește "extragerea unei rădăcini a puterii n-a" de la a. Aceasta este una dintre cele două operații care sunt inverse la exponentiare [3]. și anume, găsirea bazei gradului b de la exponentul cunoscut n și rezultatul ridicării la puterea a = b n>. A doua operație inversă, logaritm. găsește exponentul printr-o bază și un rezultat cunoscut.
Rădăcini de gradul al doilea și al treilea sunt utilizate în mod special deseori și, prin urmare, au nume speciale [3].