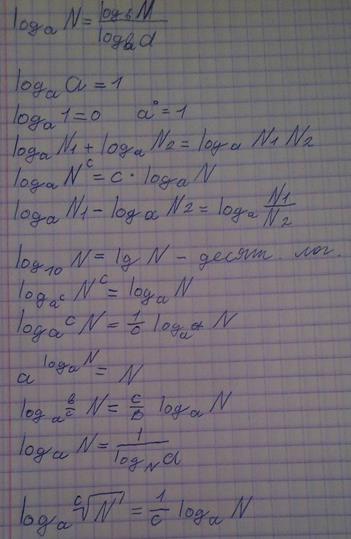un m. a n = a (m-n) (pentru un nu egal cu zero);
(a / b) n = (a n) / (b n) (pentru b nu egal cu zero);
a 0 = 1 (pentru un nu egal cu zero);
Aceste proprietăți se vor păstra pentru orice număr a, b și orice număr întreg m și n. Este de remarcat și următoarea proprietate:
Dacă m> n, atunci m> a n. pentru un> 1 și un m
Este posibilă generalizarea noțiunii de grad al unui număr în cazul în care numerele raționale sunt exponentul unei puteri. În același timp, aș vrea să văd că toate proprietățile enumerate mai sus sunt îndeplinite sau cel puțin unele dintre ele.
De exemplu, dacă proprietatea (a m) n = a (m * n) este îndeplinită, următoarea egalitate ar păstra:
Această egalitate înseamnă că numărul a (m / n) trebuie să fie rădăcina n-a unui m.
Puterea unui număr a (mai mare de zero) cu exponentul rațional r = (m / n), unde m este un număr întreg, n este un număr întreg mai mare decât unul, este numărul n√ (a m). Pe baza definiției: a (m / n) = n√ (a m).
Pentru toate r pozitive, gradul de zero este determinat. Prin definiție, 0 r = 0. De asemenea, rețineți că pentru orice întreg, orice numere naturale m și n, și pozitive și adevărate ecuația următoare: a (m / n) = a ((mk) / (nk)).
De exemplu: 134 (3/4) = 134 (6/8) = 134 (9/12).
Din definiția unei puteri cu un exponent rațional rezultă în mod direct că pentru orice a și orice rațional pozitiv r numărul a r este pozitiv.
Transformări identice ale expresiilor care conțin o diplomă cu un exponent rațional.
Grade cu indicatori reali
Să fie dat un număr pozitiv și un număr real arbitrar. Numărul este numit grad, numărul este baza gradului, numărul este numit exponent.
Prin definiție,
Dacă și sunt numere pozitive și sunt numere reale, atunci sunt valabile următoarele proprietăți:
Proprietățile unei puteri cu un exponent real
Proprietățile unei puteri cu un exponent real
Pe o putere cu exponenți reali, toate proprietățile puterilor cu exponenți raționali sunt transmise.
1)
2)
3)
4)
5)
6)
7) pentru orice x real,
8) Dacă Dacă atunci
Conceptul logaritmului unui număr
B pe baza a este exponentul la care va fi ridicată baza a. astfel încât numărul b este obținut.
Identitatea logaritmică de bază
Aceasta este identitatea logaritmică de bază.
Această identitate rezultă din definiția logaritmului: deoarece logaritmul este un exponent (n), atunci ridicând la această putere numărul a, obținem numărul b.
Proprietățile de bază ale logaritmilor
Proprietățile de bază ale logaritmilor