Diagrama de la acțiunea forței unitare la punctul A este prezentată în Fig. 7,15 g
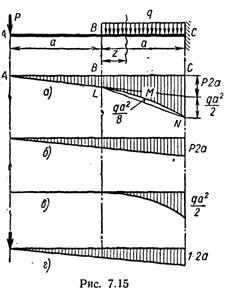
Pentru a determina deplasarea verticală la punctul A, este necesară multiplicarea diagramei de sarcină pe diagramă de la forța unității. Cu toate acestea, observă că suprafața totală a diagramei curbei de soare cu came se obține nu numai de acțiunea unei sarcini uniform distribuite, ci și de acțiunea unei forțe concentrate P. Ca urmare, zona BC nu va mai fi o curbă parabolică elementar prezentată în tabelele 7.1 și 7.2, și în În esență, o diagramă complexă pentru care datele acestor tabele sunt nevalide.
Prin urmare, este necesară realizarea unei stratificări a diagramei complexe din Fig. 7.15 și diagramele elementare prezentate în Fig. 7.15, b și 7.15, c.
Schema din Fig. 7.15, b a fost obținut numai din forța concentrată, diagrama din Fig. 7.15, c - numai prin acțiunea unei sarcini uniform distribuite.
Acum puteți multiplica diagramele utilizând tabelul. 1 sau 2.
Pentru a face acest lucru, multiplicați diagrama triunghiulară din Fig. 7.15, b pentru diagrama triunghiulară din Fig. 7.15, d și adăugați la acesta rezultatul multiplicării diagramei parabolice din Fig. 7.15, în diagrama trapezoidală a secțiunii aeronavei din Fig. 7.15, r, deoarece pe secțiunea AB coordonatele diagramei din Fig. 7.15, c sunt egale cu zero.
Acum prezentăm a doua metodă de multiplicare a diagramei. Luați în considerare din nou diagrama din Fig. 7.15, a. Să luăm originea în secțiunea V. Vom arăta că în curba momentelor LMNizgibayuschie pot fi obținute ca suma algebrică a momentelor de încovoiere linia LN corespunzătoare și îndoire diagrame momentul LNML parabolice, la fel ca și pentru un simplu fascicul de lungime și încărcate uniform distribuite de sarcină q:
Cea mai mare ordonată din mijloc va fi
.
Pentru probă, scriem expresia reală a momentului de încovoiere în secțiune la o distanță z din punctul B
Acum scriem expresia momentului de încovoiere din aceeași secțiune, obținută ca suma algebrică a ordonatelor liniei LN și parabola LNML.
Ecuația liniei LN
unde k este panta acestei linii drepte
În consecință, ecuația momentelor de încovoiere obținută ca suma algebrică a ecuației liniei LN și a parabolului LNMN are forma
care coincide cu expresia (A).
ar trebui să se înmulțească trapezoid BLNCna diagrama trapez a unei unități pe porțiunea de soare multiplicată cu diagramele regula Vereshchagin (vezi. Fig. 7,15 g) și înmulțirea rezultatului scade diagrama parabolic LNML (zona
) pe același trapez din schema unității. Acest mod de stratificare a diagramelor este deosebit de avantajos atunci când graficul curbilinar al diagramei se află pe una din secțiunile medii ale fasciculului.
Exemplul 7.7. Determinați mișcarea verticală și unghiulară a fasciculului de consolă în punctul unde se aplică sarcina (Figura 7.16).
Soluția. Se compară diagrama momentului de încovoiere pentru starea încărcăturii (figura 7.16, a).
Pentru a determina deplasarea verticală, selectați starea auxiliară a fasciculului cu o forță unitară la punctul de aplicare al sarcinii.
Construim diagrama momentelor de îndoire a acestei forțe (figura 7.16, b). Determinați mișcarea verticală prin metoda lui Mora
Valoarea momentului de încovoiere din sarcină
Valoarea momentului de încovoiere de la forța unitară
Înlocuim aceste valori ale lui MP și MiPo pentru semnul integrat și integrăm
Același rezultat a fost obținut anterior într-un mod diferit.
O valoare pozitivă de deformare indică faptul că punctul de sarcină P se deplasează în jos (spre forța unitară). Dacă am trimis forța unității de jos în sus, am avea Mi = 1z și, ca urmare a integrării, am fi primit o deviere cu un semn minus. Un semn minus ar indica faptul că mișcarea nu este sus, ci în jos, așa cum este.
Acum calculam integralele Mohr prin înmulțirea diagramelor cu regula Vereshchagin.
Deoarece ambele diagrame sunt simple, nu contează din ce diagramă să se ia zona și de la care la ordonată.
Zona diagramei de sarcină este
Centrul de greutate al acestei diagrame este situat la o distanță de 1/3 l de etanșare. Determinați ordinea diagramei momentului de la forța unitară, situată mai jos
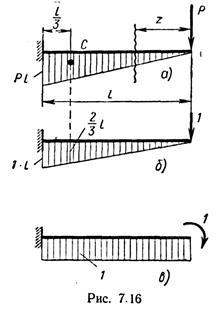
centrul de greutate al diagramei de transport de marfă. Este ușor de văzut că este egal cu 1 / 3l.
Același rezultat se obține din tabelul integralelor. Rezultatul înmulțirii diagramelor este pozitiv, deoarece ambele diagrame sunt situate la baza barei. În consecință, punctul de aplicare a sarcinii este deplasat în jos, adică prin direcția acceptată a forței unității.
Pentru a determina deplasarea unghiulară (unghiul de rotație), selectăm starea auxiliară a fasciculului, în care un moment concentrat egal cu unitatea acționează la capătul fasciculului.
Se compară diagrama momentului de încovoiere pentru acest caz (figura 7.16, c). Determinați deplasarea unghiulară, înmulțind diagramele. Zona diagramei de marfă
Ordonatele diagramei din momentul unității sunt peste tot egale cu unitatea. În consecință, unghiul de rotație dorit al secțiunii este
Deoarece ambele diagrame sunt situate din partea de jos, rezultatul multiplicării diagramelor este pozitiv. Astfel, secțiunea de capăt a fasciculului se rotește în sensul acelor de ceasornic (în direcția momentului unității).
Exemplu: determinați prin metoda Mora-Vereshchagin deformarea la punctul D pentru fasciculul prezentat în Fig. 7.17 ..
Soluția. Construim o diagramă stratificată a momentelor din sarcină, adică, construim diagrame separate de la acțiunea fiecărei sarcini. Pentru a facilita înmulțirea diagramelor, este de dorit să se realizeze diagrame stratificate (elementare) în raport cu secțiunea a cărei deviere este determinată în acest caz în ceea ce privește secțiunea D.
În Fig. 7.17, a arată diagrama momentului de încovoiere din reacția A (secțiunea AD) și sarcina P = 4 T (secțiunea DC). Diagramele sunt construite pe o fibră comprimată.
În Fig. 7.17, b prezintă diagrame în momentele de reacție (porțiunea BD) din stânga sarcină distribuită uniform (porțiunea AD) și de la o sarcină distribuită uniform care acționează pe porțiunea BC. Această diagramă este prezentată în Fig. 7.17, b în secțiunea DC de mai jos.
Apoi, vom selecta starea auxiliară a fasciculului, pentru care în punctul D, unde este determinată deformarea, aplicăm o forță unitară (figura 7.17, c). Diagrama momentului forței unitare este prezentată în Fig. 7.17, g. Înmulți acum diagramele de la 1 la 7 pe diagramele 8 și 9, folosind tabelele de înmulțire a diagramelor, luând în considerare semnele.
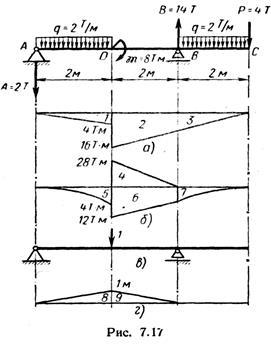
În această diagramă, situat pe o parte a fasciculului, multiplicată cu semnul plus, și diagrame sunt situate pe laturile opuse ale fasciculului înmulțit cu semnul minus.
Când se înmulțește diagrama 1 și diagrama 8, obținem
Înmulțind diagrama 5 cu diagrama 8, obținem
Înmulțirea diagramelor 2 și 9 dă
Înmulțim diagramele 4 și 9
Înmulțiți diagramele 6 și 9
Rezumând rezultatele multiplicării diagramelor, obținem
Semnul minus arată că punctul D nu se mișcă în jos, deoarece forța este direcționată, dar în sus.
Același rezultat a fost obținut mai devreme pe ecuația universală.
Desigur, în acest exemplu ar putea stratifica epure numai în zona AD, deoarece zona DBsummarnaya diagrama rectilinie și nu trebuie exfoliate. Pe secțiunea BC, nu este necesar un pachet, deoarece din forța unității din această secțiune diagrama este zero. Stratificarea diagramei în secțiunea BC este necesară pentru a determina deformarea la punctul C.
Un exemplu. Determinați deplasările verticale, orizontale și unghiulare ale secțiunii A a tijei sparte, prezentată în Fig. 7.18, a. Rigiditatea secțiunii verticale a barei este EJ1, rigiditatea secțiunii secțiunii orizontale este EJ2.
Soluția. Construim diagrama momentelor de încovoiere din sarcină. Este arătat în Fig. 7.18, b (vezi Exemplul 6.9). Pentru a determina deplasarea verticală a secțiunii A, selectăm starea auxiliară a sistemului prezentat în Fig. 7.18, c. La punctul A se aplică o singură forță verticală orientată în jos.
Diagrama momentelor de încovoiere pentru această stare este prezentată în Fig. 7.18, c.
Determinați deplasarea verticală prin metoda Mora, utilizând metoda de multiplicare a diagramei. Deoarece pe tija verticală în starea auxiliară, diagrama M1 este absentă, atunci vom înmulți doar diagramele legate de tija orizontală. Zona diagramei este luată din starea încărcăturii și ordonata este preluată din starea auxiliară. Deplasarea verticală este
Deoarece ambele diagrame sunt situate mai jos, rezultatul multiplicării este luat cu semnul plus. În consecință, punctul A se deplasează în jos, adică se îndreaptă o forță verticală a unității.
Pentru a determina deplasarea orizontală a punctului A, selectăm o stare auxiliară cu forța unității orizontale orientată spre stânga (figura 7.18, d). Diagrama momentului pentru acest caz este prezentată acolo.
Înmulțim diagramele lui Mp și M2 și obținem
Rezultatul multiplicării diagramelor este pozitiv, deoarece multiplii sunt localizați pe aceeași parte a tijei.
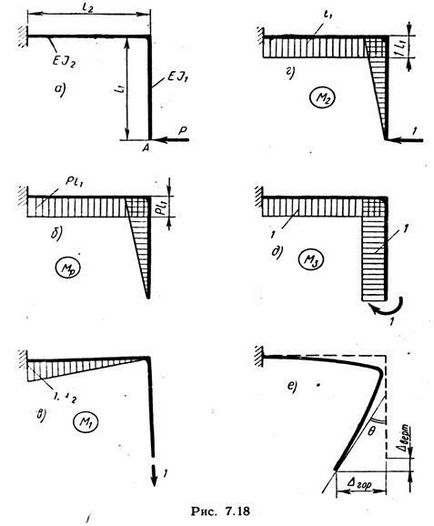
Pentru a determina deplasarea unghiulară, selectăm starea auxiliară a sistemului din Fig. 7.18.5 și compilați diagrama momentului de încovoiere pentru această stare (în aceeași figură). Înmulțiți diagramele MP și M3:
Rezultatul multiplicării este pozitiv, deoarece diagramele înmulțite sunt situate pe o parte.
Prin urmare, secțiunea A se rotește în sensul acelor de ceasornic
Aceleași rezultate s-ar obține atunci când se utilizează tabele
multiplicarea diagramelor.
Forma tijei deformate este prezentată în Fig. 7.18, e, în timp ce mișcările sunt mult mai mari.
Feodosiev VI Rezistența materialelor. 1986
Belyaev N.M. Rezistența materialelor. 1976
Rabotnov Yu.N. Mecanica unui solid deformabil. 1988