Pe baza unor sarcini practice de modelare, este posibil să se stabilească o serie de proprietăți ale rețelelor Petri care caracterizează comportamentul sistemelor simulate.
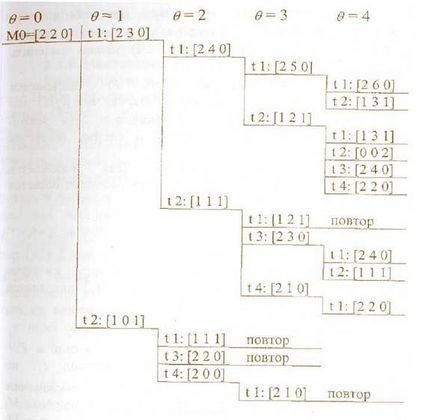
Proprietatea de limitare. Poziția pi în rețea P N = P, T, F, Mo> se consideră limitată dacă pentru orice marcare M realizabilă în rețea există k astfel încât # 956; i ≤ k. Se consideră că o rețea PN este limitată dacă toate pozițiile ei sunt limitate. Rețeaua prezentată în Figura 2.1 nu este limitată, deoarece Creștere posibilă # 956; Un simbol special este utilizat pentru a desemna marcarea fără balamale # 969; Astfel, pe arborele de marcare (Figura 2.2) putem distinge marcajul M = [1, # 969 ;, 0].
R pornește (PN, M) pentru
Proprietatea de securitate. O rețea PN este numită sigură dacă, pentru orice etichetare posibilă I ≤ 1 pentru toate i = 1. n. Astfel, într-o rețea securizată, vectorul de etichetare constă doar din zero și unul (este un cuvânt binar).
Proprietatea conservatoare. Se consideră că o rețea este conservatoare dacă suma chips-urilor în toate pozițiile rămâne constantă atunci când rețeaua
Proprietatea vieții. Să analizăm acum proprietățile tranzițiilor. Tranziția tj în rețea PN = # 920 ;, P, T, F, M0> numit potențial în viață dacă există realizabil de la Mo marcare M“, unde tj poate lucra. Dacă tj este potențial în viață, în orice PN atins de marcare, este numit un trai. Tranziția ie. non potențial în viață la marcajul inițial M0 numit mort la acest marcaj. Mo etichetare, în acest caz, se numește tj - un mort-end. Dacă marcajul este tj-blocaj pentru toate j = l. m, atunci se numește un sfârșit mort. Când marcajul de blocare nu poate declanșa nici o tranziție. Pe arborele de marcare, marcajul de blocare este o foaie.
Se consideră că o tranziție este stabilă dacă nici o altă tranziție nu o poate priva de oportunitatea de a lucra dacă există condiții necesare pentru aceasta.
Secvența marcajelor M0, M1. M r. în care Mk + 1 = # 948; k), k = 0,1. p formează un ciclu dacă M0 = Mp. Fiecare secvență corespunde unei secvențe de cuvinte în limba liberă a rețelei Petri.