Dat fiind: avem un triunghi, știm doar coordonatele vârfurilor sale. Avem un punct, știm coordonatele lui.
Ce trebuie să știți: trebuie să stabiliți apartenența unui punct la un triunghi.
Acest articol discută mai multe metode diferite pentru a determina dacă un punct aparține unui triunghi.
În această metodă, sunt localizate mai întâi zonele a 3 triunghiuri care formează punctul dat cu fiecare parte a triunghiului. În cazul nostru (fig.1), acestea sunt triunghiurile ABP, BCP, CAP și zonele lor s1, s2, s3, respectiv.
Apoi, există aria triunghiului ABC însuși.
Zonele găsite sunt comparate - dacă suma de 3 pătrate este egală cu aria întregului triunghi, atunci punctul aparține triunghiului. Când se compară, de regulă, se specifică o eroare.
Din moment ce știm doar coordonatele punctelor, atunci toate zonele sunt găsite după formula lui Heron. din abundența operațiunilor devine clar de ce această metodă este foarte consumatoare de timp.
Cea mai simplă implementare a algoritmului:
Totul este relativ!
Deci, în cazul figurii 3, punctul trebuie să stea pe partea stângă a vectorilor care aparțin triunghiului.
A treia metodă pe care o acopăr pentru mine este cea mai interesantă.
Ideea aplicării sale apare dacă vă uitați la triunghi ca o jumătate de paralelogramă ...
Am verificat mai întâi această metodă pe hârtie. După toate optimizările formulelor, cum sa întâmplat toate acestea, l-am implementat în cod, unde sa dovedit a fi destul de reușită și productivă. Deja mai eficient decât cele 2 metode anterioare:]
1) plasăm un punct al triunghiului în coordonate (0; 0);
2) cele două părți care ies din acest vârf sunt reprezentate ca vectori.
Astfel, din toate acestea, apare un sistem de condiții simple pentru găsirea punctului P între vectorii b și c (Figura 4)
Prin cod, se poate observa că există noi coordonate ale punctelor B și C, care sunt simultan vectori b și c (Figura 4). Și noile coordonate ale punctului P sunt vectorul (Px, Py). Apoi vine formula, pe care am redus-o anterior la forma generală și simplificată.
Numărul de operațiuni de bază este de 13 (+4). Deloc deloc rău:]
Aceasta este o metodă destul de bine cunoscută, mai ales când se determină dacă un punct aparține unor poligoane. Adesea, această metodă se numește "trasarea fasciculului", deși acest lucru nu este în întregime corect, deoarece ray tracing este calculul razei de lumină în scena 3D.
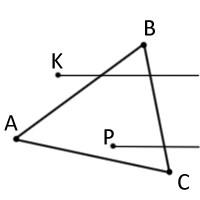
Linia de fund este că din acest punct o rază este lansată de-a lungul oricărei axe în orice direcție.
Apoi sunt verificate intersecțiile cu laturile poligonului și sunt numărate intersecțiile.
Astfel, dacă numărul de intersecții este egal, atunci punctul se află în afara poligonului, dacă numărul nu este numărare, atunci punctul se află în interiorul.
Figura 5 prezintă două puncte experimentale P și K, la grinda de la un punct de intersecție cu laturile P ale triunghiului, astfel încât punctul P aparține figurii, un punct K nu este norocos - ea a avut două intersecții.
Se pare că este simplificat în mod normal (pentru un triunghi vreau să spun), dar mi se pare ceva mai atent și ...
Și așa, avem aproximativ 30 de operațiuni.
Ei bine, aici ajungem la cele mai interesante! Cine este mai rapid și mai puternic. ]
Am testat următorii parametri (deși toate depind de procesor):
- numărul de repetări ale algoritmului pentru 1 simulare = 4 milioane.
- numărul de simulări pentru fiecare algoritm = 1000.
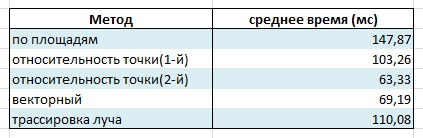
Ei bine, să spun, metoda vectorială este bună)
Cu el, desigur, concurează a doua cale de relativitate a punctului, dar principala diferență este că pentru rel. punctele au nevoie de o orientare strictă a laturilor triunghiului, iar pentru vector nu este important, deci este mai abruptă)