Mutarea unui punct material
Lăsați punctul material să se deplaseze de-a lungul axei X tot timpul într-o direcție. Apoi, deplasarea acestui punct material în intervalul de timp $ \ Delta t = t_2-t_1 $ este segmentul $ \ Delta x = x_2-x_1 $. Dacă punctul material se deplasează tot timpul într-o direcție, atunci traiectoria traversată ($ \ Delta s $) este egală cu magnitudinea deplasării:
\ [Delta s = \ stânga | \ Delta x \ dreapta | \ stânga (1 \ dreapta). \]
Dacă punctul se mișcă mai întâi într-o singură direcție, se oprește și se mișcă în direcția opusă (de exemplu, corpul se mișcă vertical în sus), apoi calea este egală cu suma modulelor de deplasare în ambele direcții:
\ [Delta s = \ left | \ Delta x_1 \ right | + \ left | \ Delta x_2 \ right | + \ dots \ left \
Determinarea vitezei medii
Viteza medie ($ \ left \ Langle v \ dreapta \ rangle $) dintr-un punct de material într-un interval de timp $ \ Delta t $ numit cantitatea fizică, care este raportul dintre mișcare, organismul sa angajat la această perioadă de timp:
\ [\ left \ langle v \ right \ rangle = \ frac \ stânga (3 \ dreapta). \]
Direcția vitezei medii este aceeași cu cea a deplasării.
Unitatea de viteză este viteza unei astfel de mișcări, la care deplasarea unui punct pe unitate de timp este egală cu o unitate de lungime:
Unitatea de viteză (inclusiv viteza medie) în Sistemul Internațional de Unități (SI) este metru pe secundă:
Viteza medie cu mișcare variabilă
Cu mișcare neuniformă, valoarea vitezei medii depinde foarte mult de alegerea intervalului de timp pentru mișcarea corpului.
Luați în considerare mișcarea unui corp care cade liber în jos. Legea mișcării este:
Pentru momente de timp $ t_1 = 0.1 \ $ c coordonatele corpului (înlocuim timpul $ t_1 $ în formula (4)) este: $ x_1 = 0,049 \ $ m; pentru $ t_2 = 0,2 \ $ c $ \ x_2 = 0196 $ m $ în timp ce \ la stânga \ Langle v \ dreapta \ rangle $ în intervalul de timp de la $ t_1 = 0,1 $ s la $ t_2 = 0,2 \ $ c va fi:
Dacă luăm în aceeași perioadă a corpului în cădere liberă de la $ t_1 = 0,7 $ s la $ t_2 = 0,8 \ $ c, viteza medie va fi egal cu $ \ left \ Langle v \ dreapta \ rangle = 7,4 \ frac $.
Viteza medie a mișcării uniforme
Numai dacă mișcarea este uniformă, viteza medie este o constantă și nu depinde de alegerea intervalului de timp în care corpul se mișcă. Cu o mișcare uniformă a punctului material de-a lungul axei X, ecuațiile cinematice pentru deplasare sunt scrise astfel:
Să găsim viteza medie a mișcării, folosind definiția (3) și expresia (6):
Pentru a evalua valoarea numerică a vitezei medii în practică folosesc următoarea definiție $ \ left \ Langle v \ dreapta \ rangle $: viteza medie egală cu traiectoria (e) raportul proydonnogo la momentul (t), care a fost cheltuită pentru circulație:
\ [\ left \ langle v \ right \ rangle = \ frac \ stânga (7 \ dreapta). \]
Viteza medie determinată în acest fel este o cantitate scalară.
Exemple de sarcini cu o soluție
Sarcină. Pietonul a petrecut prima jumătate a timpului său în mișcare cu o rată de $ v_1 = 5 \ frac $, a doua jumătate a timpului în care călătorea la $ v_3 = 3 \ frac $. Care este viteza medie a mișcării unei persoane?
Soluția. Să facem un desen.
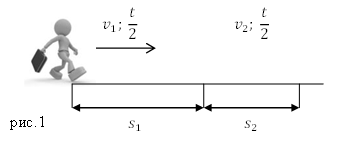
Pentru a rezolva problema, folosim formula care determină viteza medie:
\ [\ left \ langle v \ right \ rangle = \ frac \\ stânga (1.1 \ right), \]
unde traseul este alcătuit din două secțiuni de trafic:
Și de condiția problemei:
\ [s_1 = v_1t_1 = v_1 \ frac \ stânga (1.3 \ dreapta) \ și \\] \ [s_2 = v_2t_2 = v_2 \
Înlocuim laturile din dreapta ale expresiilor (1.2) - (1.4) în definiția vitezei medii (1.1) și luăm în considerare faptul că $ t = t_1 + t_2 $:
Să calculăm viteza medie a unui pieton:
\ [\ left \ langle v \ right \ rangle = \ frac = 4 \ (\ frac). \]
Răspuns. $ \ left \ langle v \ dreapta \ rangle = 4 \ frac $
Sarcină. Care este viteza medie pe care materialul o avea în intervalul de timp $, dacă ecuația vitezei sale are forma:
\ [v \ stânga (t \ dreapta) = A + Bt + Ct ^ 2 \ \ stânga (l \
Soluția. Ca bază pentru rezolvarea problemei, folosim formula ($ t = \ tau $):
\ [\ left \ langle v \ right \ rangle = \ frac \\ stânga (2.1 \ dreapta). \]
Să găsim calea punctului material, ținând cont de ecuația de viteză din datele problemei:
Înlocuind partea dreaptă a lui (2.2) în (2.1), avem: