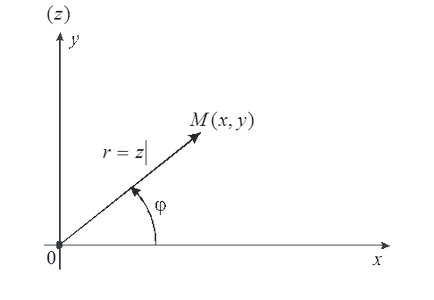
Unghiul dintre axa reală Ox și vectorul se numește argumentul numărului complex z. . Valoarea cuprinsă în decalaj se numește valoarea principală a argumentului (notația -arg z):
Valoarea principală a argumentului numărului complex z poate fi determinată de formula
Definiția. Vezi intrarea
se numește forma trigonometrică a notării numărului complex z.
Notă. Numărul complex z este de asemenea scris în formă exponențială
Pentru a compara numerele complexe și a introduce doar operația de egalitate: numere complexe și sunt egale dacă părțile lor reale și imaginare sunt respectiv :. Egalitatea numerelor scrise în formă trigonometrică este formulată după cum urmează: dacă modulele lor sunt egale, iar argumentele sunt legate de
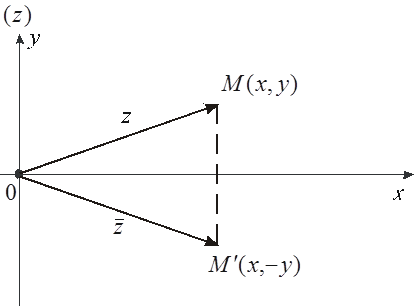
Definiția. Două numere complexe se numesc numere conjugate complexe. Pentru a face acest lucru, utilizați notația și (figura 2).
16.1.2. Acțiunile de adunare, scădere, înmulțire și divizare.
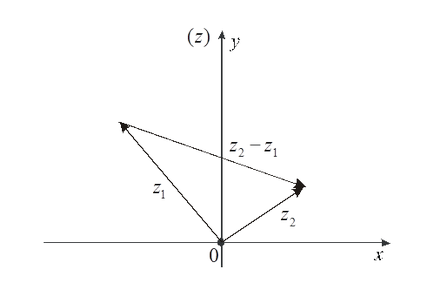
- Pentru a adăuga două numere complexe (de exemplu), este necesar să adăugați separat piesele reale și imaginare, care vor fi părțile reale și imaginare ale sumei numerelor. Din formulele (1.7) și (1.8) găsim
Prin produsul numerelor complexe și (denotat) se înțelege numărul complex z. egal
Un număr complex special și este determinat prin acțiunea de multiplicare și poate fi realizat prin formula
Lucrurile practice sunt diferite. Deoarece prin formula (1.10), este convenabil să se efectueze divizarea prin următoarea formulă:
Astfel, operațiunile de adăugare și multiplicare a numerelor complexe fac obiectul celor cinci legi cunoscute ale aritmeticii:
1. (comutativitatea adăugării);
2. (asociativitatea adăugării);
3. (comutativitatea multiplicării);
4. (asociativitatea multiplicării);
5. (distributivitatea multiplicării în raport cu
Formula (1.10) "dezvăluie semnificația" unității imaginare ". Astfel, multiplicarea numerelor complexe se face conform regulilor obișnuite ale algebrei cu înlocuirea cu -1.
Să dăm o soluție de "exemple tipice" conceptelor introduse mai sus.