- tipul de localizare a traiectoriilor sistemului autonom al ecuațiilor diferențiale obișnuite de ordinul doi:
(*)
. G este un domeniu de unicitate în vecinătatea unui punct singular (echilibrul poziției) x0. Acest tip este caracterizat după cum urmează. Există o vecinătate a punctului x0 astfel încât pentru toate traiectoriile sistemului începând de la ambele semiprejectori pozitivi și negativi ieșind (ei lasă orice compact cu timpul). Singurele excepții sunt patru traiectorii (cu un complot parazitar). Pentru două dintre ele, semitractoarele negative sunt ieșite, iar semimargătoarele pozitive se învecinează cu punctul x0. pentru celelalte două - dimpotrivă. Primele două separatrice sunt numite. stabil, al doilea două - instabil. Separaturile stabile, fiind completate de punctul x 0, formează o curbă netedă care trece prin x 0 - o varietate stabilă de șa. Separatoarele separate instabile, împreună cu punctul x 0, formează un distribuitor neted al șei. În acest caz, și punctul x 0 însuși.
Șaua x 0 este instabilă conform lui Lyapunov. Indicele său Poincare este -1. Pentru un sistem (*) de clasă cu matrice nonzero A = f '(x 0), punctul de odihnă x 0 este C. în cazul în care valorile proprii l1, l2 ale matricei satisfac condiția ll, 2 <0 (простое С. рис. 1, где x0 = 0), но может быть С. и в тех случаях, когда или l1 =l2 =0. В любом из этих случаев сепаратрисы С. касаются в точке х 0. направлений, определяемых собственными векторами матрицы А.
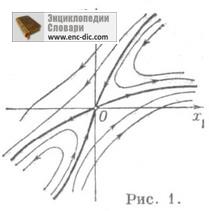
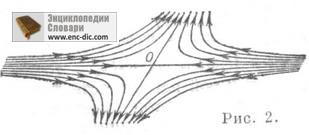
În cazul în care sistemul (*) este liniar (f (x) -A (x-x0), A este o matrice constantă cu valori proprii l1, 12), atunci punctul x0 este C numai dacă l1 l2 <0. Сепаратрисы седла х 0 в этом случае прямолинейны, а все остальные траектории (отличные от точки х 0 ). суть аффинные образы гипербол вида (рис. 2).
Termenul "C." este folosit aici pentru orice locatie a traiectoriilor (*) în vecinătatea U izolat punct de repaus x 0, pentru k-setat de la 0 până la un punct x este adiacent doar un număr finit de traiectorii, și fiecare dintre ele fiind completate punctul x0. se referă la o anumită direcție în ea (m-separatrix C.). S. este numit. și anumite tipuri de puncte de odihnă ale sistemelor autonome ale ecuațiilor diferențiale ordinare de ordin
Lit. a se vedea art. Un punct singular al ecuației diferențiale. AF Andreev.
Enciclopedia matematică. - M. Enciclopedia sovietică IM Vinogradov 1977-1985