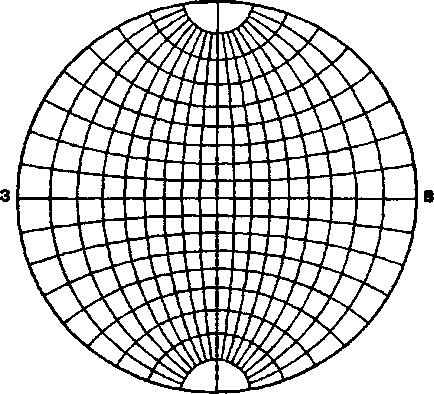
Proiecțiile stereografice se caracterizează prin cele două cele mai importante
Orice cerc desenat pe o sferă este de asemenea prezentat pe proiecția stereografică printr-un cerc (într-un caz particular, printr-o linie dreaptă);
Pe proiecția stereografică, relațiile unghiulare nu sunt distorsionate.
Unghiul dintre polii fețelor de pe sferă (măsurat de-a lungul arcurilor de cercuri mari) este egal cu unghiul dintre proiecțiile stereografice ale acelorași arce.
Proiecția gnomasterografică este folosită cel mai adesea pentru imaginea de poliedra cristalină. În acest caz, nu este proiectat un polyhedron, ci complexul său polar.
Planul proiecției gnomosteografice este același plan ecuatorial al sferei de proiecție, ca și proiecția stereografică.
Pentru a construi o proiecție gnomosteografică a cristalului, este necesar pentru toate
se fixează perpendicularii și continuă până când se intersectează cu suprafața sferei de proiecție descrisă în jurul centrului de greutate al cristalului și
oferind posibilitatea de a trasa o linie care să lege punctele de polaritate cu punctul de vedere.
Proiecțiile gnomosteografice ale direcțiilor (marginile cristalului) sunt reprezentate în același mod ca și normalele față de fețe.
Se formează complexul de fețe, normalele la care se află în același plan
Zona de proiecție a fețelor aparținând unei zone este situată pe una
arcul unui cerc mare.
Net Wolf în cristalografie - stereogram gradul grilă pe teren, la un punct de vedere asupra ecuator și paralelele grila sfery.Meridiany Wolf joacă doar un rol de sprijin ca o proiecție a arcele de cercuri mari și mici.
Punctul de intersecție al meridianului zero cu circumferința rețelei Woolf (# 966; = 0, # 961; = 90). Eroarea grilei Woolf este de 2 °.
Metoda a fost inventată de cristalograful Georgi Vulf.
Cu ajutorul grila Wolfe se poate construi o proiecție stereografică a unui punct dat de coordonatele sale sferice # 966; și # 961;
Grilă Wulf permite grafic, fără calcule suplimentare, să rezolve multe probleme de cristalografie geometrică legate de caracteristicile unghiulare ale cristalelor.
12. Forme simple de polyhedra cristalină. principiile retragerii acestora.
Formele simple de cristale sunt un set de fețe identice cristalografice care coincid unele cu altele sub acțiunea operațiilor de simetrie ale unei clase date. Ie Doar forma perfectă a unui cristal numit un poliedru, dintre care toate fețele pot fi obținute de la o față folosind transformările de simetrie inerente simetrie grup de puncte de cristal. Pentru toate fețele formei simple a unui cristal ideal, ratele de creștere sunt aceleași, toate fețele sunt cristalografice, atât în proprietățile lor fizice cât și chimice.
Dacă setul de planuri de formă simplă nu închide spațiul, atunci se numește deschis. Formele deschise sunt caracteristice cristalelor de sindroame inferioare și sunt posibile în toate sistemele, cu excepția cristalelor cubice. Dacă spațiul este închis, se formează un polyhedron convex, care este o formă închisă. Un astfel de polidron este numit izoehedron, adică "echin".
Forma formei simple și a numărului de fețe depind de modul în care aceste fețe sunt aranjate în ceea ce privește elementele de simetrie.
În cazul în care mai multe tipuri de muchii pot fi identificate printre fețele poliedrului, care diferă în formă și / sau dimensiune, atunci vorbim despre câteva forme simple, sau o combinație de forme simple. Orice poliedr complex poate fi împărțit într-un număr finit de forme simple, fiecare dintre ele caracterizată prin proprietățile sale.
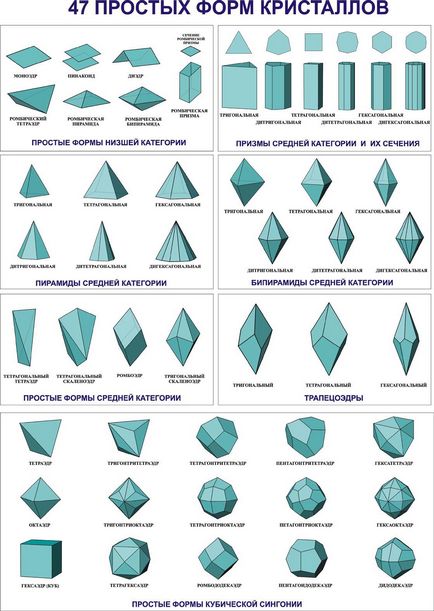
Concluzia formelor simple constă în căutarea unor forme de poziții generale și diverse specifice fiecărui grup de cristale. Nume forme simple derivate din numerele grecești rădăcină (mono - una, di - două, etc.) și cuvintele „EDR“ - legați sau „rutului“ - unghi.