copie
1 LUCRĂRI DE LABORATOR 9 OPERATORI LINEARI ȘI FUNCȚIONALE ÎN SPAȚIILE NORMALE. NORMA OPERATORULUI LINEAR ȘI FUNCȚIONAL. DEFINIREA EQUACATIILOR DIFERENTIALE. Spațiu vectorial și spațiu în același câmp (= R sau C). Se afișează. cu domeniul de definiție D () și intervalul de valori R () este numit un operator liniar de la in dacă pentru orice, y și. ) (y) y (aditivitate); ) () (omogenitate). Denumim prin (,) mulțimea tuturor operatorilor liniari din 6 al căror domeniu de definiție coincide cu E. Pentru (,) și definiți operatorii, () prin formule. def def (); (). Apoi (,) devine un spațiu vectorial. În cazul particular, atunci când (câmpul este un spațiu vectorial!), Elementele (,) sunt denumite functionalals linear. Acum presupunem că normele i (i,) sunt definite pe i, adică spații normate (Norm). Definiția. Operatorul (,) este numit operator limitat de la 6 dacă există o constantă c astfel încât pentru orice avem egalitatea c. Definiția. Norma operatorului (,) este numărul def sup. Se poate arăta că c este o definiție. există o limită exactă inferioară a mulțimii tuturor constantelor
2 THEOREM. Lăsați (,), unde, Norm. Apoi următoarele afirmații sunt echivalente. ) operatorul este un operator continuu de la; ) operatorul este un operator limitat de la; ). Haideți, (,), unde, Norm. Următoarele relații sunt valide :); ); ). Prin urmare, în cazul în care, operatorii delimitate, atunci operatorii sunt, de asemenea, delimitate. Prin urmare, dacă L (,) indică mulțimea tuturor operatorilor liniare limitate de la 6, atunci L (,) de către subspațiul vectorial (,). este THEOREM. Dacă Norm și Banach (Ba), atunci L (,) Ba. Tot ceea ce sa spus este valabil și pentru funcționari. În acest caz, norma este activă, deci funcția f (,) se spune că este limitată la Norm dacă există o constantă c astfel încât f () c pentru orice. Apoi, norma f funcțională este numărul def f f f () dacă c. f () c. De la Ba, apoi de teorema L (,) Ba. Definiția. Spațiul Banach L (), constând din funcții liniare limitate, va fi notat cu * și va fi numit spațiul adjoint la E. Referințe: [] pag. 9-56; [] pagina 8-5; [5]
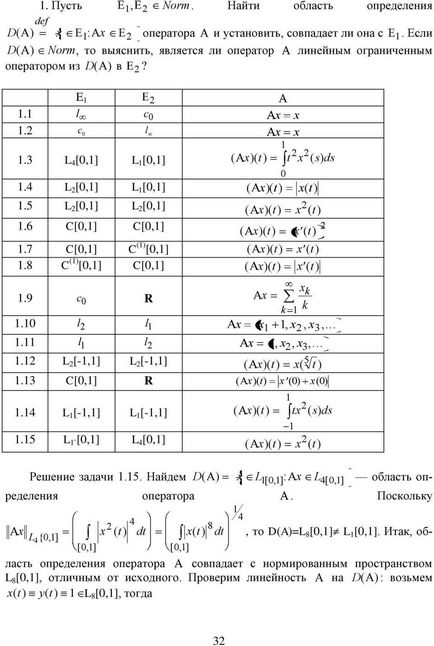
3. Să presupunem că Norm. Găsiți domeniul def D (). operator și să stabilească dacă se potrivește cu. Dacă D () Norm, atunci să aflăm dacă operatorul este un operator liniar delimitat de la D () la? E. lc. c l. L [,] L,] () (t) t (s). (T) (t), () (t) (t), [], [(] t). C (,) () [,] () (t) (t) .8 C () [,] (t). L l. L [-,] L [-,] () (t) (5 t). C [,] R () (t) () (). L [-,] L -,] () (t) t (s) .5 L, [], () (t) (t) Soluția problemei. Să găsim D () L [,]. L [,] domeniu de definire a operatorului. Deoarece 8 (t) (t), rezultă că D (A) = L L
dacă ($ this-> show_pages_images $ page_num doc ['images_node_id'])
4 (y) y. Prin urmare, operatorul nu este liniar pe D (), și deci limitat. -5. Această formulă oferă un operator liniar delimitat. Dacă operatorul este limitat, găsiți norma. Operatorul de multiplicare. C [,] C [,] () (t) (t t) (t). C [-,] C [,] () (t) (t t) (t). L [,] L,, () (t) t (t). (T) (t) .5 L [-,] [-,] () (t) t (t) (t) () () () () t (t) .7 L [,] L [,] () (t) (t) .9 L [-,] L [-,] () (t) t (t). C () [-,] C [,] () (t) si t (t). L [,] L,, () (t) t (t). C [-,] C [-,] () (t) (t) (t), t [, [(t t) (t), t [,]. C [,] L,, () (t) t (t) t (t), t [,]. L [-,] L [-,] () (t), t [, [Soluția problemei. Domeniul operatorului D () L [-,] (produsul (t) printr-o funcție continuă nu "deduce" acest produs din L [-,]). Linearitatea operatorului este evidentă. Deoarece pentru L [-,]
5 L t t t [,] () () L
6. L [,] L [,] () (t) t (t). L [-,] L [,] () (t) t (t) Soluția problemei. Lăsați L [-,]. Apoi, t (t) L [,] u t t u u u (u) (u) (u) du u (u) du L [,]. Din ultima relație rezultă că D () L [-,]. Este evident că operatorul este liniar, iar din inegalitatea de mai sus rezultă că A este limitat și. Luați în considerare o secvență de funcții (t) (t) L [,]. Apoi, [L], sup [L], sup [u] du L [,] L [,] sup 5 So 5 sup 5 5. Ținând cont de cel precedent, avem. Operatorii în spații secvențiale l l (.) 5
7. ll (.). c c (.). L l. 5 l l. 6 l l. 7 l l. 8 c c. 9 c și c. si. l l (.). l c. L l. l c (.). L l. unde M, N Soluția problemei. Deoarece pentru supor, D () l și liniaritatea operatorului sunt ușor de verificat. Din aceasta avem supa I. Prin definirea limitei superioare exacte, pentru că există astfel de I. Atunci pentru L (l) l și ll I. Depășind limita din I, adică, în ultima inegalitate. sup 5. Operatorul integral produce 6
8 5. L [,] L [,] () (t) ts (s) 5. L [,] L [,] () (t) (t) s (s) 5. C [,] L [ ,] () (t) (ts) (s) 5. L [,] C [-,] () (t) ts (s) 5,5 L [,] lt. t (t), L [,] l t (t). t (t), t (t), L (t) t (s) 5.8 L [,] ,] () (t) ts (s) 5. L [,] L [,] () (t) (t) s (s) 5. C [,] L [,] () (t) sig ( (s) t () 5. L [-,] L [,] () (t) (t) s (s) s) 5. L [,] lt (t). t (t). 7
9 Soluția problemei 5. Lăsați L [,]. Apoi Lt (t) (t) L. [,] Prin urmare, D () L [,] și liniaritatea operatorului rezultă din liniaritatea integrala. De la inegalitatea stabilită, rezultă că 8. Pe de altă parte, dacă (t) (t), atunci, și L, [,] sup, l supt sup () 8. Prin urmare, Let Ba, K sau C. Această formulă dă o funcționalitate liniară delimitată f. În cazul unui răspuns pozitiv, găsiți-o normă. f 6. c C () lim 6. l R f () 8
(6) (6) (6) () () () (6) R f () 6. C f () i 6. C f () 6. c R f () lim 6. l C f () Soluția problemei 6. Linearitatea funcționalului este ușor de verificat. Să presupunem că l. Apoi, aplicând inegalitatea Cauchy-Bunyakovskii, avem. Prin urmare, D (f) 1, funcționalitatea f este legată de l și f este constantă c. Arătăm că este cel mai mic dintre toate posibilitățile în inegalitate (). Pentru a face acest lucru, este suficient să specificăm un element nonzero l astfel încât () să devină un lanț de egalități. Egalitatea în () poate fi încălcată după aplicarea inegalității Cauchy-Bunyakovskii. Acesta din urmă nu încalcă egalitatea dacă * 9
11 N. f () * * Noi luăm, apoi pentru * (.), 8. Astfel, f. (7), (), (), (), (), (t) 7,5 L [,] t (t) 7,6 L [-,] ,] Rf () t (t) 7,9 C () [,] C f () () i () 7. C () [,] Rf () (t) (t) 7. C () [ -,] C f () () 7. C () [,] C f () i () () 7. L [,] Rf () t (t) 7. L [,] C f () (t) f * și
12 Soluția problemei 7. Linearitatea unei funcții rezultă din liniaritatea integrală. Să presupunem că L [,]. Apoi, după schimbarea variabilelor din integrale și apoi aplicarea inegalității Cauchy-Bunyakovskii, obținem f () t (t) u t udu u u u u u u () (). () Prin urmare, D (f) l, funcțional este mărginit și f. Luați * (u) u (de ce?), Apoi din () avem * * f () u u du u du. Prin urmare, rezultă că este posibilă constanta c. Prin urmare, în f () este cea mai scurtă dintre toate variantele Varianta Varianta Varianta Varianta Varianta Varianta post Varianta Varianta Varianta Varianta Varianta Varianta Varianta Varianta Varianta Varianta
13 Varianta Varianta Varianta Varianta Varianta Varianta Varianta Varianta Varianta Varianta D D O T L N I E A L H N E W A D A B u și v P R O F E S H J. Demonstrați că f funcțional. (t) (t) R (t) C () [,] este continuă. 5. Dovedeste ca f. (t) (t) R este liniar și nelimitat pe subspațiul liniar C () [,] al spațiului normat C [,]. 6. Considerăm operatorul (.) (.). În ce condiții este limitată de l? Găsiți-i norma. 7. Fie operatorul multiplicării printr-o funcție măsurată limitată a () care acționează în spațiul L p (,). Dovedeste ca este limitata si isi gaseste norma. 8. Găsiți norma operatorului de identitate care acționează din Lp [a, b] în Lq [a, b] pentru p q.
LABORATORUL OPERATORULUI SPECTRUM. O N E N E D E F G H I O T I O T IO S I S Let. Un operator liniar delimitat într-un spațiu Banach pe un câmp. C. Definiție. Un punct C este numit regulat
1 Funcții continue pe interval (Bolzano-Cauchy, Weierstrass, teoremele lui Cantor). Functionale continuu pe un compactum. 1.1 Teorema privind valorile intermediare Teorema 1 (Bolzano-Cauchy) Fie o funcție f continuă pe intervalul [a, b], unde f (a) f (b). Apoi pentru orice număr C cuprins între f (a) și f (b) există un punct γ (a, b) astfel încât f (γ) = C. Dovada. Să presupunem, de exemplu, f (a) = A 0. Este suficient să se arate că există un γ punct (a, b), care g (γ) = 0. Impartim intervalul [a, b] punctul x 0 pe două egale lungimea segmentului, atunci fie g (x 0) = 0, și deci punctul y dorit = x 0 este găsit, sau g (x 0) 0 și apoi la capetele unuia dintre lacunele rezultate g ia valori de semne diferite, mai precis, pe capătul din stânga este mai mic decât zero, în dreapta - mai mult. Denumim acest segment [a 1, b 1] și îl împărțim din nou în două segmente de lungime egală și așa mai departe. Ca rezultat, fie un număr finit de pași pentru a ajunge la punctul y dorit, în care g (γ) = 0, sau de a obține secvența de segmente nested [a n, b n] cu o lungime care tinde la zero, astfel încât g (a n)