Scurtă descriere a documentului:
În sesiunile anterioare ați învățat regulile de găsire a funcției derivate, învățat despre aplicarea derivatului pentru studiul funcției pe monotonicitate și extremum; învățat să găsească tangenta graficului funcției.
Reamintește regulile pentru calcularea instrumentelor derivate:
Derivatul oricărui număr este zero.
Derivatul lui x este unul.
Derivatul unui plus este egal cu ka.
Derivatul unității împărțit la X este egal cu minus unul, împărțit cu X în pătrat.
Rădăcina derivată a lui X este egală cu una împărțită de două rădăcini de X.
Derivatul sinusului X este egal cu cosinusul X.

Derivatul cosinusului X este minus X.
Derivatul lui x în puterea lui en este egal cu en înmulțit cu x la puterea minus unu.
Uneori este necesar să rezolvăm și să inversăm problemele, de exemplu, pentru a restabili legea mișcării la o viteză cunoscută.
În matematică este obișnuită invocarea operațiunilor reciproce inverse cu nume speciale.
De exemplu, o operație inversă la înmulțire este împărțirea.
Funcționarea extragerii rădăcinii pătrată este inversarea împărțirii.
Procesul de găsire a derivatului unei funcții date se numește diferențiere, iar operația inversă este o integrare (procesul de găsire a unei funcții cu privire la un derivat dat).
Aceasta este funcția, care acționează ca strămoș al derivatului unei funcții date, este numită de obicei un antiderivativ.
Definiție: functia y egal mare Aeff al X se numește o funcție y primitivă egală mică Aeff de X la un interval predeterminat X este mare, în cazul în care pentru orice X aparținând acestui decalaj, următoarea egalitate:
Diferența de care aparține X, de obicei, nu este indicată, ci este implicită.
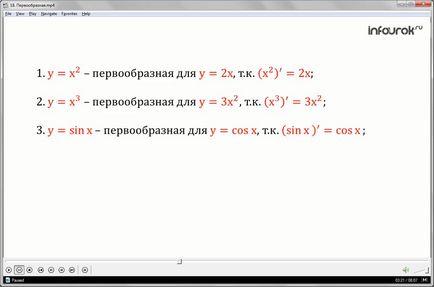
1. Funcția igk, egală cu x în pătrat, este antiderivativă pentru funcția igk, egală cu două ix, deoarece pentru orice ix egalitatea este adevărată: derivatul ux din pătrat este egal cu două ix.
2. Funcția y, egală cu X în cub, este o funcție primitivă y egal cu trei X în piață, ca și pentru toate egalitatea X: X derivat din cub este egal cu trei X la pătrat.
3.Funktsiya y egal cu sinusul X, este o funcție primitivă y egal cu cosinusul X, ca și pentru orice X egalitatea: derivata sinusului este cosinusul X X.
4.EDITING y egal cu rădăcina pătrată a X, este o funcție primitivă y egal cu unul împărțit la rădăcina pătrată a două X, în intervalul de la zero la infinit, deoarece pentru orice X este mai mare decât zero, egalitatea: rădăcina derivat al X este egal cu unu, împărțit în două rădăcini de X.
Cunoscând formulele pentru găsirea derivatelor, nu este dificil să faci un tabel de antiderivative:
1. Valoarea zero este egală cu o constantă.
2. Prima unitate este x.
3. Începutul pentru x este egal cu x în pătrat, împărțit la doi.
4. Primul pentru funcția x în puterea en, en aparține setului de numere naturale, este egal cu x la gradul en plus unu, împărțit de en plus unu.
5. Primul caracter pentru funcția 1, împărțit la X în pătrat, este minus unul, împărțit la X.
6. Primul pentru funcția 1, împărțit prin rădăcina lui X, este două rădăcini de X, iar X este mai mare decât zero.
7. Funcția primitivă pentru funcția sinusoidală este egală cu minusul cosinusului x.
8. Cosinul invers al funcției cosinus este egal cu sinusul lui x.
9. Primul pentru funcția unu, împărțit de sine în pătratul lui X, este egal cu minus cotangent X.
10. Primul pentru funcția unul, împărțit de cosinus în pătratul x, este egal cu tangenta lui X.

Să luăm în considerare exemplele privind găsirea antiderivantei a diferitelor funcții.
Dovedeste ca functia este un antiderivativ al functiei. dacă antiderivativul funcției este egal cu x în a șasea putere, funcția însăși este egală cu șase X în a cincea putere.
1. Prin definirea unui primitiv, functia y egal mare Aeff al X se numește o funcție primitivă y egală mică Aeff de X la un interval predeterminat X este mare, în cazul în care pentru orice X aparținând acestui decalaj, egalitatea.
2. Vom găsi derivatul eF cu formula pentru găsirea derivatului unei funcții de putere. este șase X în a cincea putere.
Am obținut egalitatea a două expresii, prin urmare, prin definiția antiderivativului, funcția ef este mare, egală cu x în a șasea putere, este antiderivantă pentru funcția ef mică, egală cu șase x în a cincea putere.
Pentru o functie (igk, egala cu ef de la x mica) pentru a gasi antiderivative daca
(ef de la X este egal cu minus unul, împărțit cu X în cub).
1. Prin definirea unei grade cu un exponent negativ intreg, reprezentam expresia minus unul, impartit cu X in cub, sub forma: minus x in minus gradul III.
2. Prin formula pentru găsirea unei funcții de putere antiderivativă, găsim antiderivativul pentru funcția ef de la ux, egal cu minus x în minus gradul 3.
Obținem, minus X în minus trei plus unul, împărțit la minus trei plus unu.
Simplificând expresia, avem un minus negativ de minus doi, împărțit la minus doi, reducând minusul, obținem: X în gradul minus doi, împărțit la două.
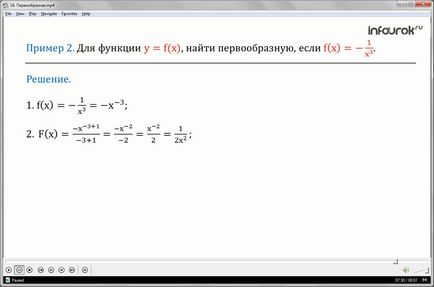
Prin definiția unei puteri cu un exponent negativ întreg, reprezentăm expresia în forma: una, împărțită de două X într-un pătrat.
Astfel, primitivul pentru funcția ef de la x este unul mic, egal cu minus unul, împărțit de X într-un cub, este o funcție a lui ef mare, egal cu unul, împărțit de două xs într-un pătrat.