Construirea unei proiecții stereografice a unui cristal
Conform legii constantei de unghiuri dihedral, constantele caracteristice ale cristalelor sunt magnitudinile lor unghiulare. Prin urmare, din setul de metode de proiectare în cristalografie, cele care dau un concept precis al colțurilor pe cristale sunt utilizate preponderent. În acest sens, proiecțiile stereografice sunt deosebit de convenabile. "Stereos" (greacă.) - spațială.
Luăm un punct O ca centrul proiecțiilor (figura 9)
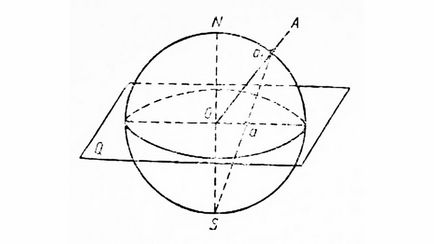
O rază arbitrară descrie o sferă în jurul valorii de O, numită bila de proiecții. Prin același punct O tragem un plan orizontal Q, care este planul proiecțiilor.
Ca urmare a intersecției suprafeței sferice cu Q, avem un cerc mare (liniile de intersecție a suprafeței sferei cu planurile care trec prin centrul său) corespunzând ecuatorului mingii de proiecție și reprezentând cercul proeminențelor.
Diametrul vertical al bilei NS perpendicular pe Q se numește axa de proiecție. O astfel de axă intersectează bila de proiecții la două puncte - N și S. Unul dintre aceste puncte (polul sudic al balonului de proiecție - S) este un punct de vedere.
Dacă doriți să descrieți proiecția stereografică a oricărei direcții sau a unui avion, le transferăm în paralel cu noi înșine pentru a trece prin centrul O.
Luați în considerare obținerea unei proiecții stereografice a unei anumite direcții OA (figura 25). Pentru a face acest lucru, vom continua această direcție până când proeminențele se vor intersecta cu suprafața mingii. Fie ca punctul a1 să fie rezultatul intersecției OA cu suprafața mingii.
Punctul a este punctul de intersecție al S a1 cu planul Q, este proiecția stereografică a direcției OA. Astfel, proiecția stereografică a direcțiilor este reprezentată de puncte.
Gasim proiecția stereografică a planului R. Mai întâi transferăm R paralel cu noi către centrul proiecțiilor, continuăm până când se intersectează cu suprafața mingii de proiecție (Fig.10).
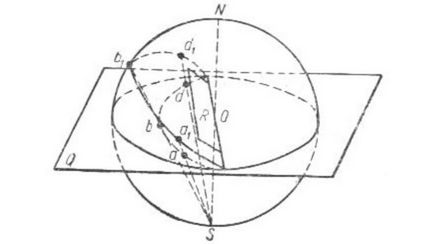
Ca rezultat al intersecției, obținem pe minge un arc de cerc mare a1 in1d1 ... Conectăm toate punctele din acest cerc cu liniile de vedere S1 S1 Sd1 cu punctul S. Aceste raze formează conul proeminent cu vârful S.
Rezultatul intersecției conului proiectat cu planul de proiecție Q corespunde proiecției stereografice a planului dat.
O teoremă este cunoscută conform căreia proiecția stereografică a unui cerc este, de asemenea, un cerc.
În general, proiecțiile stereografice ale planelor sunt reprezentate de arce circulare.
Să începem proiectarea cristalelor folosind proiecție stereografică.
Să presupunem că ni se dă un anumit poliedru cristalin. Luăm un punct în interiorul lui, de exemplu centrul de greutate, în spatele centrului proiecțiilor (figura 27). Din acest punct descriem o suprafață sferică - bilele de proiecții - cu o rază arbitrară. Prin centru desenăm un plan orizontal de proiecții Q și suntem de acord să desenăm întregul desen pe el.
Punem perpendiculare din centrul O pe toate fețele de cristal și le extindem la intersecția cu suprafața sferei. Ca urmare a intersecțiilor pe o suprafață sferică, apar mai multe puncte. De exemplu, în Fig. 27, iar fața obișnuită la fața A dă punctul a1 pe suprafața mingii.
Fig. 27. Proiectarea cristalului prin metoda de proiecție stereografică (a); imaginea proiecțiilor fețelor A, B, C și D pe planul Q (b)
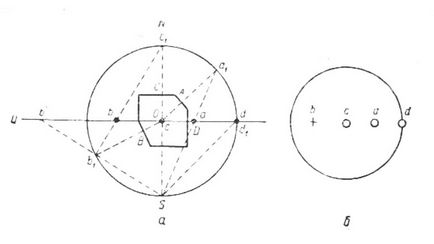
Toate punctele găsite ar trebui transferate în planul orizontal al proeminențelor Q. În acest scop, polul sud al mingii S este luat ca un punct de vedere și conectăm punctele aflate pe sferă cu acesta.
Ca urmare a intersecției razelor cu planul desenului obține noi puncte corespunzătoare proiecției stereografica a normalele la fețele. Astfel, în această proiecție fețele sunt reprezentate prin puncte (litera a. - proiecție Stereografic normal la feței A (Fig.27) normalele intersectându proiecții cu bile în emisfera inferioară sunt proiectate în afara acestui interval (de exemplu, normal la Fig.27 OM) Inconvenientele. ultima construi face pentru transferul de vedere normal al S în polul nord al domeniului de aplicare al N. în acest caz, proiecția și fețele inferioare vor fi în intervalul de proiecții.
Pentru a distinge între proiecțiile normalelor față de fețele superioare și inferioare, primele sunt notate cu cercuri, iar cele din urmă prin cruci.
1. Feretele orizontale sunt proiectate în centrul cercului de proeminențe (de exemplu, fața C, figura 27);
2. Feretele verticale sunt proiectate pe cercul propriu al proiecțiilor (de exemplu, fața D);
3. Fețele oblice sunt proiectate în interiorul cercului de proiecții (de exemplu fețele A și B). Cu cât este mai înclinată panta feței (adică, cu cât unghiul dintre față și axa de proiecție este mai mic), cu atât mai aproape de punctul care îl proiectează este cercul proeminențelor. Și, cu cât este mai mare fața (cu cât este mai mare unghiul specificat), cu atât mai aproape de punctul corespunzător cu centrul cercului.