Cifrele de construcții de proiecție plane (t. E. Cifrele, toate punctele din care se află într-un plan, de exemplu, un pătrat, cerc, elipsa și altele. D.) este redus la construcția proeminențelor o serie de puncte, segmente de linie dreapta si linii curbe care formează contururile figurilor proiecțiilor. Cunoscând coordonatele nodurilor, de exemplu, un triunghi, se poate construi proiecțiile acestor puncte, atunci laturile proeminenței și astfel se obține forme de proiecție.
Desenele care conțin proiecțiile triunghiului au fost deja întâlnite (de exemplu, figurile 110, 112, etc.). Dacă comparăm fig. 110 și 112, se poate vedea că în Fig. 110 una dintre proiecții, punem partea frontală, prezintă partea "din față" a triunghiului și partea orizontală - partea "din spate". Și în Fig. 112 fiecare dintre proeminențe reprezintă un triunghi pe aceeași parte. Ordinea de traversare a nodurilor poate servi drept semn: în Fig. 110 pentru proiecția frontală în sensul acelor de ceasornic (numărând de la A la C) și pentru orizontală în sens invers acelor de ceasornic; în Fig. 112 pentru ambele proiecții, traversal într-o direcție - în acest caz în sensul acelor de ceasornic.
În cazul general, în sistemul π1. π2. π3 proiecțiile unui poligon sunt, de asemenea, poligoane cu același număr de laturi; planul acestui poligon este un plan de poziție generală. Dar dacă în sistemul π1. π2, ambele proeminențe, de exemplu, triunghiurile sunt un triunghi, atunci planul său poate fi un plan de poziție generală sau de proiectare a profilului: în Fig. 112 este planul poziției generale, iar în Fig. 127 - Proiectarea profilului. Determinantul servește, așa cum sa spus pe p. 52 în explicația din Fig. 127, orizontală (sau față): dacă proeminențele sale pe π1 și π2 sunt reciproc paralele, atunci planul este proiectat în profil (figura 127); dacă nu este paralelă, atunci planul poziției generale (de exemplu, figurile 112, 115, stânga).
Dacă proiecția unui poligon pe π1 sau π2 este un segment de linie dreaptă, atunci planul acestui poligon este perpendicular pe π1 sau π2, respectiv. De exemplu, în Fig. 123 planul triunghiului se proiectează pe orizontală, în Fig. - proiectarea frontală.
Figura, situată paralel cu planul proiecțiilor, este proiectată pe ea fără distorsiuni. De exemplu, toate elementele triunghiului CDE, prezentate în Fig. 133, sunt proiectate pe patrat. π2 fără distorsiuni; cercul prezentat în Fig. 140, proiectat la pl. π1 fără distorsiuni. -
Dacă planul figurii nu este paralelă cu planul de proiecție pentru a determina forma naturala (m. E. Fără distorsiuni) a figurii metodele specificate în continuare se aplică, capitolul V. Desigur, s-ar putea acum, fără să știe aceste metode de a construi, de exemplu, aspectul natural al triunghiului prezentat în Fig. 112, determinând lungimea fiecărei laturi ca lungime a segmentului (vezi § 13) și apoi construind un triunghi de-a lungul segmentelor găsite. În același timp, unghiurile triunghiului dat ar fi de asemenea determinate. Acesta este cazul, de exemplu, atunci când trasați o curățare
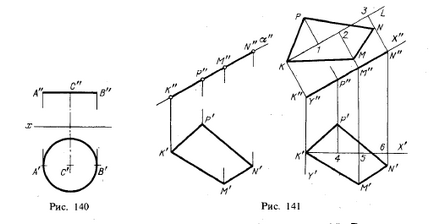
suprafața laterală a piramidei, prisma etc. (a se vedea în continuare § 44). Dacă poligonul este situat în planul de proiectare, puteți construi forma sa naturală, așa cum se arată în Fig. 141.
Să presupunem că este necesară determinarea formei naturale a KPNM quadrangle, localizată în proiecția pl. α. Apoi, așa cum se arată în Fig. 141 în dreapta, se poate lua în planul figurii două axe de coordonate dreptunghiulare cu originea cel puțin la punctul K; 2. Axa abscisei ordonata perpendicular pe π2 (proiecția acestei axe K „Y“, K'Y „), trage o linie dreaptă KL (acest lucru se poate face, de exemplu, paralel cu«X») și puneți-l pe K1 = K„R ", K2 = K" M ", K3 = K" N ". Apoi, pe perpendicularele la linia KL la punctele 1,2 și 3 amâna segmentele P1 = R'4, M'5 și M2 = N3 = N'6. Quadrilateralul KMNP construit în acest fel este o formă naturală a celei date.
Atunci când rezolvăm multe probleme, întrebarea despre ce poziție ocupă o figură plană cu privire la planurile proiecțiilor devine importantă. De exemplu, luați în considerare construirea a patru puncte remarcabile ale unui triunghi.
Deoarece segmentul de linie diviziune în spațiu corespunde jumătății aceeași divizie a porțiunii de proiecție (vezi. § 12), construcția punctului de intersecție al medianele triunghiului 1) poate fi produs în figură, în toate cazurile în mod direct. Destul (Fig. 142), mediana cheltui pe fiecare dintre proiecțiile triunghiului și punctul de intersecție al medianele sale vor fi determinate. Astfel, este posibil să se limiteze construcția ambelor proeminențelor numai o mediană (de exemplu, A'D „și A«D») și o a doua proeminență mediană (de exemplu, V«E»); în intersecția A "D" și B "E" obținem punctul M ", iar pe acesta găsim punctul M 'pe A'D'.
De asemenea, ați putea construi doar unul dintre medianele triunghiului, găsiți un punct M pe acesta pe baza proprietății acestui punct cunoscut din geometrie (se împarte fiecare median în raport de 2 1).
Construcția punctului de intersecție al celor trei altitudini ale unui triunghi 2) și punctul perpendicular pe laturile triunghiului trasate prin mijlocul 3) legate de liniile perpendiculare reciproc.
1) Punctul de intersecție al medianilor este centrul de greutate al triunghiului.
2) Ortocenterul triunghiului.
3) Centrul cercului circumscris.
În § 15 au fost specificate condițiile în care segmentele de linie perpendiculare în spațiu sunt proiecțiile sale sunt de asemenea perpendiculare pe segmentele, dacă planul triunghi paralel cu planul de proiecție (de exemplu, CDE triunghi în Fig. 133), apoi, scăzând perpendicularele din punctele C „D“ și E "pe părțile opuse, obținem proiecțiile înălțimilor triunghiului, Dar într-un triunghi de poziție generală, acest lucru nu se poate face,
În cazul particular, când o parte a triunghiului este paralelă cu pătratul. π1; iar celălalt PIBpp paralel, π2 (fig, 143), având C "F" perpendicular "B" A și V'E 'perpendiculară pe A'C' ajunge în spațiul și CF⊥AV BE⊥AS; Punctul de intersecție a înălțimilor sa dovedit a fi construit fără tehnici speciale.
În cel mai general caz, pentru realizarea liniilor perpendiculare pe un desen de proiecție, trebuie să recurgem la metode speciale, care vor fi descrise ulterior.
Construirea punctul de intersecție al Bisectoarele triunghiului 1) poate fi produs direct numai în cazuri speciale, poziția triunghi în raport cu planurile de proiecție. Acest lucru se datorează faptului că un unghi de împărțire în două proiecție de împărțire în două răspunde în spațiul numai în cazul în care unghiul dintre laturile sunt la fel de înclinate în raport cu planul de proiecție pe care proiecții produse unghi de împărțire în două (a se vedea. § 15).
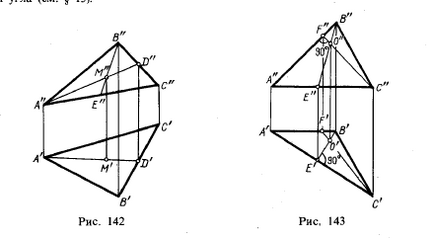
Atunci când se construiește proiecțiile unui poligon, este necesar să se acorde atenție faptului că condiția de a găsi toate punctele unei figuri date în același plan
În Fig. 144 sunt proiecții complet orizontale ale unor pentagon ABCDE și proiecții frontale ale celor trei vârfuri: A ", B" și E ", dreapta
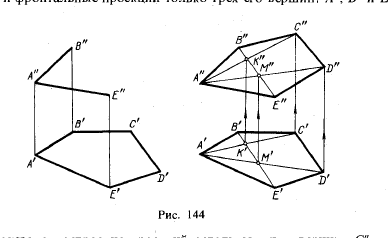
Figura 144 prezintă construcția proeminențelor celor două vârfuri rămase, C "și D", pentagonul, astfel încât punctele C și D se află într-un plan definit de trei puncte A.
1) Centrul cercului inscripționat.
B și E, este necesar ca acestea au fost pe liniile situate în planul acestor linii sunt diagonala AC, AD și BE, proiecția orizontală pe care putem construi. Pe proiecția frontală a pentagonului putem trage doar în „E“, dar în planul pentagonului sunt punctele de intersecție a diagonalelor K și M, proeminențele orizontale (K „și M“) sunt disponibile, iar proiecția din față, obținem o dată, deoarece acestea trebuie să se bazeze pe B "E". Două puncte sunt construite proiecție frontală, iar celelalte două diagonale A „R“ și A „M“, ei trebuie să se afle punctele C „și D“, care sunt definite de proiecțiile lor orizontale.
Cercul, al cărui plan este paralel cu orice plan de proiecție, este proiectat pe acest plan fără distorsiuni (vezi figura 140, unde cercul este luat în plan orizontal). Dacă planul cercului este perpendicular pe planul proeminențelor, atunci în acest plan, cercul este proiectat sub forma unei linii drepte egale cu diametrul cercului,
Dar dacă cercul este situat într-un plan care face un unghi ascuțit cu planul de proiecție, atunci proiecția cercului este o figură numită elipsă.
O elipsă este, de asemenea, o curbă care leagă o figură de elipsă: dacă o figură de elipsă este o proiecție a unui cerc, atunci linia de elipsă este o proiecție a cercului. În următoarea discuție, atunci când vorbim de o elipsă, înțelegem proiecția unui cerc.
Elipsa se referă la numărul de curbe denumite curbe de ordinul doi. Ecuațiile unor astfel de curbe în coordonate carteziene sunt ecuațiile de ordinul doi. O curbă de ordinul doi se intersectează cu o linie dreaptă în două puncte. Apoi ne vom întâlni cu o parabolă și o hiperbolă, de asemenea curbe de ordinul doi.
O elipsă poate fi considerată drept un cerc "comprimat". Acest lucru este arătat în figura 145 din stânga. Să presupunem că segmentul OB1 al lungimii b este așezat pe raza OB și b 1) la elipsă la punctul K.
1) De la normalis (lat.) - rectiliniu.
Cum se construiesc axele unei elipse daca sunt cunoscute diametrele sale conjugate?
Lăsați jumătate diametrele conjugate CA și CB să fie obținute (Figura 148). Pentru a plota axele unei elipse:
- unul dintre semidiametrele conjugate, de exemplu CB, este rotit printr-un unghi de 90 ° față de celălalt (până la poziția CB2);
- tragem un segment AB2 și îl împărțim în două;
- Din punctul K tragem un cerc cu raza CS;
- linia definită de segmentul AB2. continuați să intersectați cu acest cerc la punctele D și E;
- tragem o linie dreaptă DC, obținem direcția axei majore a elipsei;
- conduce UE - direcția axei mici a elipsei;
- amâna C1 = AE - axa semimajor;
- amâna S3 = AD - semiaxis mic;
- am complot C2 = C1, C4 = C3, C5 = CA, C6 = CB.
Elipsa poate fi trasă prin opt puncte 1, A, 3, B, 2, 5, 4 și 6 sau construită de-a lungul unei axe mari și mici, așa cum se arată în Fig. 147.
Deci, după ce am realizat CD-ul direct și CE, am obținut indicații ale axelor mari și mici ale elipsei; punctul A, care aparține elipsei, împarte diametrul ED în două segmente, dintre care unul (AE) este egal cu semiaxisul acestei elipse, iar celălalt (AD) - cu semiaxul mic. Dacă (figura 149)
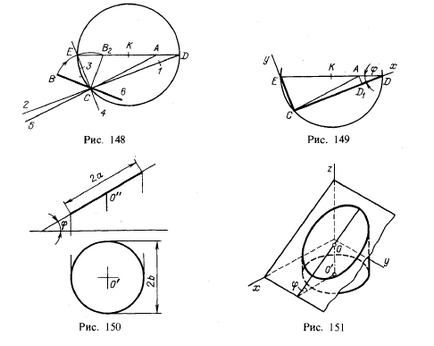
luați axele coordonatelor x și y respectiv de-a lungul liniilor drepte CD și CE și din punctul A trageți perpendicularul AD pe linia dreaptă CD, atunci coordonatele punctului A pot fi exprimate după cum urmează:
Această ecuație a elipsei, în care AE - axa semimajor și AD - axa semimajor.
În Fig. 146 a fost arătată construcția unei proiecții orizontale a cercului situată în planul înclinat față de pătrat. π1. Acum permiteți o elipsă cu semiaxe a și b să stea într-un astfel de plan. Proiecția lui poate fi uneori un cerc cu un diametru egal cu axa minoră a elipsei: acesta va fi atunci când pentru unghiul dintre planul în care se află elipsa și pătratul. π1, raportul cos? = b / a (Figura 150).
Cercul rezultat va servi drept proiecția unei serii de elipse dacă unghiul φ și dimensiunea a se schimbă, lăsând b neschimbate. Imaginați-vă un cilindru circular drept cu o axă verticală (Figura 151); Secțiunile înclinate ale acestui cilindru sunt elipse, a căror axă minoră este egală cu diametrul cilindrului.
Întrebări la §§20-21
- Cum se trasează planul de proiectare plană prin linia dreaptă în poziția generală prezentată în figură?
- Cum să construiți proiecțiile centrului de greutate într-un desen triunghi dat?
- Ce pot reprezenta proiecțiile cercului, în funcție de poziția planului său față de planul proiecțiilor?
- Poate o elipsă să fie considerată un cerc "comprimat"?
- Care este raportul de compresie al unei elipse?
- Elipsa are: a) axa de simetrie, b) centrul simetriei?
- Care diametre ale elipsei sunt numite: a) axe, b) diametre conjugate?
- Cum să construiți axele sale din diametrele conjugate date ale unei elipse?