Sistemul de coordonate al dispozitivului și sistemul de coordonate mondial
Fereastra de ieșire
Trasarea
Când nu există timp.
Când lucrați cu grafica pe calculator, trebuie să vă ocupați de două sisteme de coordonate. Primul sistem este sistemul de coordonate al dispozitivului (sau sistemul de coordonate al ecranului). Coordonatele punctului din acest sistem sunt numărul pixelilor din rândul X și numărul de linii de pixeli Y:
0 <= X <= Xmax
0 <= Y <= Ymax
Al doilea sistem de coordonate este așa-numitul sistem de coordonate mondial sau matematic. Este un sistem cartezian (x. Y), definit de programator, și este independent de un anumit dispozitiv grafic:
xmin Parametrii care definesc intervalele x și y (xmin.yom.xmax.yamax) definesc o regiune dreptunghiulară într-un spațiu matematic bidimensional. Acești parametri depind doar de sarcina specifică. Coordonatele și coordonatele mondiale ale dispozitivului sunt legate de relații simple: Formula pentru coordonata "ecranului" Y diferă oarecum de formula pentru coordonatele X, deoarece axa OY este îndreptată în jos în sistemul de coordonate al ecranului. Pentru ca, de fiecare dată când este nevoie să se convertească coordonatele de la un sistem la altul, să nu se scrie aceste expresii, este convenabil să se formalizeze calculul funcțiilor X și Y. De exemplu: Desigur, prezența a două sisteme de coordonate nu înseamnă că, în toate cazurile, fără excepție, este necesar să le folosim. Doar există situații în care este mult mai convenabil să lucrați cu coordonatele lumii, fără să gândiți cu adevărat cât de mulți pixeli pe ecran sunt orizontal și vertical. Ca exemplu de utilizare a funcțiilor de transformare a coordonatelor, luați în considerare următoarea problemă. În centrul ecranului, trebuie să afișați o anumită zonă (vezi Fig.) Și un punct al cărui coordonate sunt introduse cu
tastatură.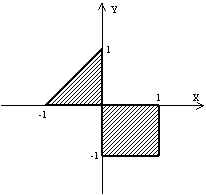
Să începem prin a spune că trebuie doar să afișăm axele de coordonate (fără marcare) pe ecran și contururile zonei respective. Acest lucru se poate face prin lucrul direct cu coordonatele ecranului. Să presupunem că rezoluția ecranului este de 640 x 480 pixeli.
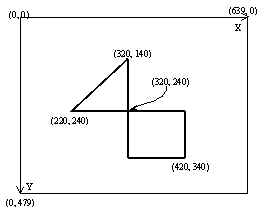
Pentru a construi axele și conturul regiunii, utilizați procedurile Line and Rectangle:
<Оси>
Linie (0,240,639,240);
Linia (320,0,320,479);
<контур>
Linia (220, 240, 320, 240);
Linia (220, 240, 320, 140);
Linia (320, 140, 320, 240);
Dreptunghi (320,240,420,340);
Odată cu construirea domeniului de probleme nu au apărut. Acum, să afișăm punctul cu coordonatele x = 0.6 pe ecran. y = -0,8. Pentru a "pune" punctul pe ecran, trebuie să apelați procedura PutPixe l. Dar procedura PutPixel. precum și alte proceduri grafice, funcționează numai cu coordonatele ecranului. Și ce coordonate ale ecranului corespund punctului (0,6, -0,8). Desigur, ele pot fi calculate:
Dar, în acest caz, este mult mai convenabil să lucrăm în sistemul de coordonate mondiale încă de la început. Definim-o, de exemplu, după cum urmează:
Să construim conturul domeniului care lucrează în sistemul de coordonate mondial, folosind funcțiile definite anterior Xs (x) și Ys (y).
Pentru a afișa un punct cu coordonatele x = 0.6, y = -0.8, este suficient să scrieți:
PutPixel (Xs (0,6), Ys (-0,8), alb);
Uneori, când construiți imagini, este necesar să împărțiți ecranul în mai multe zone dreptunghiulare (ferestre grafice), astfel încât în fiecare fereastră să puteți crea propriul dvs. imagine. În modulul GRAPH pentru aceste scopuri există o procedură specială SetViewPort:
SetViewPort (X1, Y1, X2, Y2, Integer; ClipMode, Boolean);
unde variabilele X1, Y1, X2 și Y2 specifică coordonatele diagonale ale ferestrei, iar parametrul ClipMode determină dacă o parte a imaginii care se află în afara ferestrei va fi afișată sau nu. Parametrul ClipMode poate lua două valori. Valoarea ClipOn (true) indică faptul că o parte a imaginii din afara ferestrei nu trebuie afișată, iar valoarea ClipOff (false) indică posibilitatea de a afișa imaginea unei ferestre care a căzut în afara limitelor. După efectuarea acestei proceduri, ecranul grafic este "comprimat" la dimensiunea ferestrei, cursorul curent deplasează colțul din stânga sus al ferestrei și originea este mutată acolo. Dacă parametrul ClipMode este setat la ClipOn. atunci o parte a ecranului din afara ferestrei devine indisponibilă.
Scopul ferestrei grafice poate fi folosit pentru a muta originea sistemului de coordonate al dispozitivului. Deci, dacă setați fereastra apelând
SetViewPort (GetMaxX Div 2, GetMaxY Div 2, GetMaxX, GetMaxY, ClipOff);
De asemenea, puteți lucra cu ferestre grafice fără a utiliza procedura SetViewPort. Pentru a face acest lucru, este suficient să modificați doar ușor funcțiile de transformare a coordonatelor considerate anterior.
Selectați pe ecran o zonă dreptunghiulară cu diagonală (XWmin, YWmin) - (XWmax, YWmax):
Compatibil cu această zonă este sistemul de coordonate matematice dat de parametrii xmin. Ymin. xmax și ymax. Formulele de transformare a coordonatelor în acest caz vor avea următoarea formă:
Când lucrați cu coordonatele lumii și utilizați această metodă de organizare a ferestrelor grafice, este recomandabil să includeți în program următorul bloc de descriere:
Introducere în procedurile programului SetWorldCoords și SetWindow este opțională, deoarece acțiunile lor pot fi implementate direct în blocul principal al programului. Atunci când se organizează mai multe ferestre de ieșire, se recomandă utilizarea acestor proceduri, deoarece scurtează textul programului și îmbunătățește lizibilitatea acestuia. Mai mult, în conformitate cu principiile programării structurale, este de dorit ca orice operație mai mult sau mai puțin izolată și completă să fie formalizată ca un subprogram separat.
Graficul este modul cel mai vizual de prezentare a datelor experimentale, afișarea dependenței obținute ca urmare a simulării numerice și așa mai departe. Prin urmare, construirea de diferite grafice este una dintre etapele importante în soluționarea multor probleme aplicate. Graficele pot fi de diferite tipuri: punct, liniar (sub forma unei linii întrerupte care leagă punctele individuale), poligoane, grafice sub formă de diagrame de bare (histogramă), sub formă de diagrame plăcute etc.
Luați în considerare, de exemplu, problema construirii unui grafic liniar al unei funcții arbitrare într-un interval de variație dat al argumentului. Datele inițiale din această sarcină sunt: funcția, graficul căruia se construiește, intervalele modificării argumentului a și b. și numărul de puncte N. afișate pe grafic (sau pasul de modificare a argumentului dx). La rezolvarea problemei, este de dorit urmarea următoarei secvențe de acțiuni:
- Introducerea datelor inițiale;
- tabularizarea funcției (calcularea valorilor funcției atunci când argumentul este schimbat de la a la b cu pasul dx);
- determinarea valorilor minime și maxime ale funcției pe un anumit interval;
- definirea sistemului de coordonate mondiale;
- construcția axelor de coordonate;
- reprezentând un grafic al funcției.
Luați în considerare implementarea unora dintre acțiunile de mai sus și proiectați-le sub forma unor proceduri și funcții separate. În programul principal, descriem următoarele constante și variabile:
Constanta N specifică numărul de puncte afișate pe grafic. În matricele X și Y vom pune rezultatele funcției de tabulare.
În plus, înțelegem că programul include o descriere:
- variabilele întregi XWmin, XWmax, YWmin și YWmax, care determină coordonatele ferestrei de ieșire (a se vedea mai sus);
- variabilele reale xmin, xmax, ymin, ymax, definirea sistemului de coordonate matematice;
- Procedurile SetWindow și SetWorldCoords (vezi mai sus);
- două funcții pentru transformarea coordonatelor Xs și Ys;
- intreg variabilele GrDr și GrMd, necesare pentru procedura de inițializare a graficii.
funcția F (x. real). reale;
începe
F: = expresie pentru funcția a cărei grafică urmează să fie construită;
se încheie;
Determinarea valorilor minime și maxime ale unei funcții:
Definiția valorilor minime și maxime ale funcției în acest caz este redusă la găsirea elementelor minime și maxime din matricea Y, care se obține în tabela funcției. Să proiectăm această operație ca funcții separate pentru valorile minime și maxime, respectiv:
Axele coordonatelor:
Baza pentru construirea oricăror grafice și diagrame este sistemul de coordonate. Mai jos este procedura de a construi pe ecran un sistem de coordonate carteziene cu imaginea axelor și marcajelor perimetrului. Procedura are doi parametri nx și ny, care determină numărul de curse pe axele OX și OY, respectiv.
PROCEDURE BuildCoords (nx, ny. Byte);
VAR
i. byte;
v. reale;
s. șir de caractere;
BEGIN
SetColor (alb);
Dreptunghi (XWmin, YWmin, XWmax, YWmax); <область графика>
Linia (Xs (xmin), Ys (0), Xs (xmax), Ys (0)); <ось ОХ>
Linia (Xs (0), Ys (ymax), Xs (0), Ys (ymin)); <ось OY>
SetTextStyle (SmallFont, 0,5); <выбор шрифта Small>
SetTextJustify (CenterText, CenterText); <выравнивание текста>
pentru i: = 0 până la ny-1 nu începe
v: ymin + (ymax-ymin) / (ny-1) * i;
Str (v: 5: 2, s);
Linia (XWmin, Ys (v), XWmin-5, Ys (v));
OutTextXY (XWmin-30, Ys (v), s);
se încheie;
END;
PROCEDURĂ Grafic (Culoare);
VAR i. întreg;
BEGIN
SetColor (Culoare);
MoveTo (Xs (X [1]), Ys (Y [1]));
Cercul (Xs (X [1]), Ys (Y [1]), 2);
PENTRU i: = 2 TO N DO începe
LineTo (Xs (X [i]), Ys (Y [i]));
Cercul (Xs (X [i]), Ys (Y [i]), 2);
se încheie;
END;
Procedura grafică construiește un grafic punct-la-linie al punctelor stocate în matricele X și Y. Parametrul Color specifică culoarea liniei.
Astfel, ținând cont de subrutinele discutate mai sus, programul de construire a grafurilor funcționale va avea următoarea structură:
PROGRAM Graphic_of_Function;
UTILIZĂ CRT, Grafic;
CONST
N = 50;
VAR
X, Y. array [1..N] de real;
VAR
Descrierea variabilelor XWmin, XWmax, YWmin, YWmax;
Descrierea variabilelor xmin, xmax, ymin, ymax;
Descrierea procedurii SetWorldCoords;
Descrierea procedurii SetWindow;
Descrierea funcției Xs;
Descrierea funcției Ys;
Descrierea procedurii TablFunc;
Descrierea funcției MinY;
Descrierea funcției MaxY;
Descrierea procedurii BuildCoords;
Descrierea procedurii Grafic;
VAR
a, b. reale;
GrDr, GrMd. întreg;
BEGIN
ClrScr;
Scrieți ('Introduceți limitele pentru modificarea argumentului [a, b]:');
ReadLn (a, b);
TablFunc (a, b);
GrDr: = detectează;
InitGraph (GrDr, GrMd, "C: \ TP7 \ BGI");
SetWindow (100, 50, 500, 400);
SetWorldCoord (a, MinY, b, MaxY);
BuildCoords (5, 5);
Grafic (galben);
ReadKey;
CloseGraph;
END.
Acest program poate fi modificat cu ușurință, astfel încât să traseze un grafic al punctelor date, obținut, de exemplu, ca urmare a unui experiment. Strict vorbind, nimic nu trebuie schimbat pentru acest lucru. Este necesar să se scrie o nouă procedură pentru popularea matricelor X și Y. Amintiți-vă că procedura TablFunc a făcut acest lucru înainte. Procedura de introducere a datelor se poate face după cum urmează:
După aceea, în blocul principal al programului, în loc de a apela TablFunc, trebuie să apelați procedura ReadDATA.
La prima vedere, programul de mai sus pentru construirea grafurilor liniare poate părea oarecum complicat (deși aceasta este doar o complexitate aparentă) și supraîncărcat cu diverse proceduri și funcții. Principalul avantaj al abordării și al programului în relativitatea lor universală: indiferent de funcția pe care o stabiliți, indiferent de modificările pe care le faceți în argument, programul va construi neapărat programul dorit. Iar întreaga imagine a graficului se va potrivi exact în fereastră. Fără îndoială, universalitatea trebuie plătită și, în acest caz, cu costul introducerii diferitelor variabile și subrutine. Dar, folosind arsenalul acestor subrutine, puteți construi cu ușurință pe ecran un singur grafic și câte zece, fiecare având axe de coordonate proprii. Dacă doriți, o descriere a unor subrutine (cum ar fi SetWindow, SetWorldCoords, Xs, Ys). precum și variabilele XWmin, XWmax, YWmin, YWmax, xmin, xmax, ymin și ymax pot fi emise ca un modul separat. De asemenea, puteți adăuga proceduri pentru plotarea altor tipuri de grafice. Toate acestea vor permite simplificarea în continuare a redactării programelor care prevăd construirea de grafice.
4. Când nu există timp ...
La rezolvarea diferitelor sarcini, de exemplu legate de modelarea pe calculator a anumitor procese, este adesea necesar să se afișeze grafic rezultatele obținute. În același timp, este posibil ca cerințele minime să fie stabilite pentru înregistrare, mai ales dacă rezultatele sunt intermediare. În acest caz, desigur, nu este nevoie să scrieți un program universal de complot și, prin urmare, multe din lucrurile discutate mai devreme pot fi mult simplificate.
De exemplu, luați în considerare o sarcină simplă:
Piatra este aruncată la un unghi la orizont cu viteza inițială. Este necesar să se construiască pe traiectorii de ecran mișcarea de piatră pentru diferite valori ale unghiului de aruncare.
Ecuațiile de mișcare pentru coordonatele pietrei x și y din cadrul inerțial fix au forma:
Având în vedere valorile și înălțimea maximă a pietrei deasupra orizontului și intervalul maxim al zborului, se determină:
Pentru a construi traiectoria mișcării de piatră pentru valorile date de u, este necesară schimbarea valorii t cu un anumit pas. calculați coordonatele x și y și afișați-le pe ecran. Pentru ca ecranul să se potrivească tuturor traiectoriilor cu valori diferite ale unghiului de aruncare, trebuie mai întâi să determinați intervalul maxim de zbor și înălțimea de ridicare pentru o anumită valoare. Evident, intervalul maxim de zbor va fi (la) și înălțimea maximă de ridicare (la).
Definim sistemul de coordonate carteziene (coordonatele lumii) în raport cu care vom construi traiectoriile mișcării pietrei:
xmin = 0, xmax =, ymin = 0, ymax =.
Luând în considerare formulele (1), coordonatele ecranului vor fi determinate de următoarele expresii:
unde este introdusă notația. și.
Mai jos este programul corespunzător.