Produsul matricei
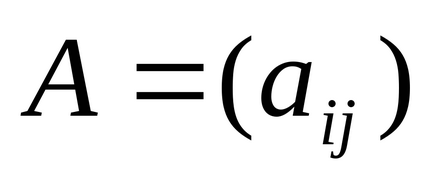
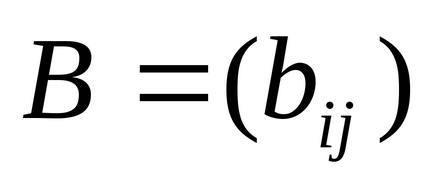
Pentru a scrie în foaia de lucru, trebuie să tastați "number" * "name
Înmulțirea vectorilor și a matricelor.
Produsul matricei
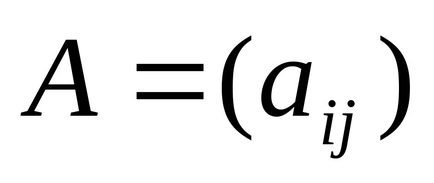

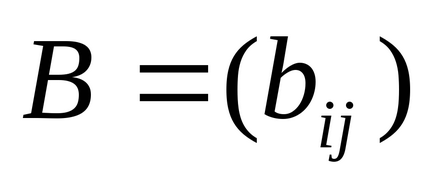

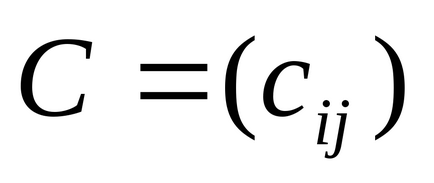
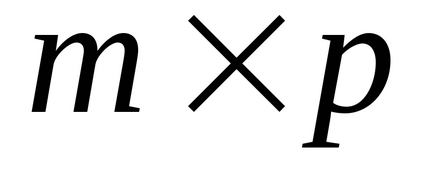
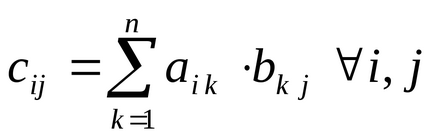
Pentru a scrie operatorul de multiplicare a matricei, puteți introduce A [Shift] * B = (egal) sau utilizați operatorul Dot Product, produsul scalar al panoului Matrix matrix.
Pentru vectori, există două tipuri de multiplicare:
- scalare multiplicare (Dot Product)
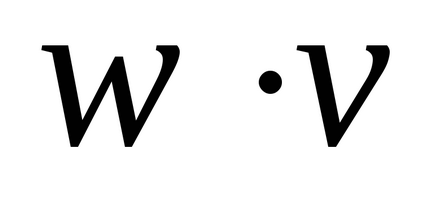
- vector de lucru (Cross Product)
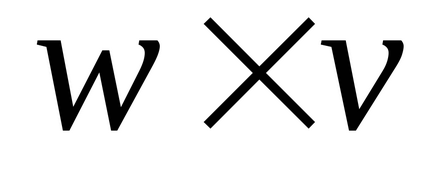
Pe foaia de lucru, produsul scalar al vectorilor este scris exact în același mod ca și în cazul matricelor.
Produsul vectorial al vectorilor necesită acces la panoul Matrix, pentru care trebuie să faceți clic pe opțiune
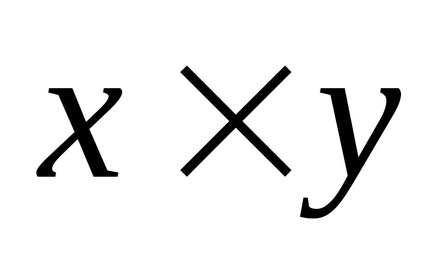
Transpunerea vectorilor și a matricelor.
Transformarea transformării matricei, în care coloanele matricei originale devin șiruri de caractere:
Transpunerea unei coloane vectoriale duce la înlocuirea acesteia cu un șir de vectori de aceeași dimensiune:
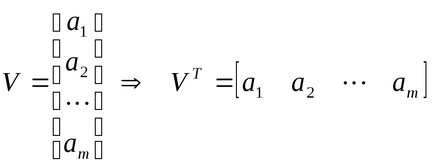
Exemple de acțiuni de bază cu vectori sunt prezentate în Fig. 3.11. Cu privire la utilizarea funcțiilor Mathcad, de exemplu, svds (v). ultima (v) este descrisă mai jos.
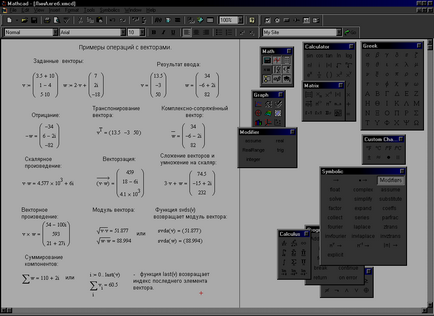
Fig. 3.11. Un exemplu de operațiuni cu vectori.
3.2.5. Matricea inversă. Determinantul matricei.
matrice
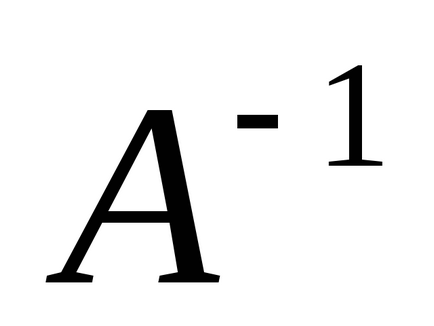
D
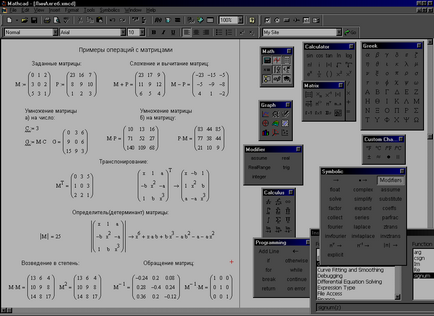
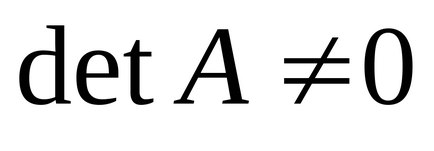
Fig. 3.12. Exemple de acțiuni cu matrice.
Determinant (determinant) al matricei pătrate
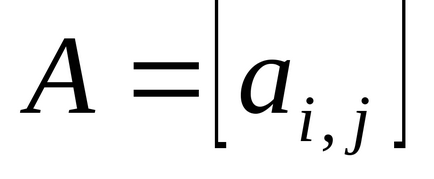
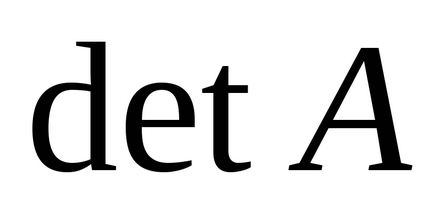
În Mathcad, există două modalități de a calcula determinantul.
În cazul în care elementele de matrice sunt ID-urile trebuie să introduceți același șablon determinant, completați-l și faceți clic pe semnul mouse-ul simbolic egal (săgeata stânga) de pe panoul de Simbolice (calcul simbolic) pentru a afișa rezultatul în formă simbolică (fig. 3.12).
3.2.6. Operatorul vectorizează.
În Mathcad există un operator numit operator de vectorizare, care este util în mod special pentru efectuarea în mod repetat a acelorași calcule.
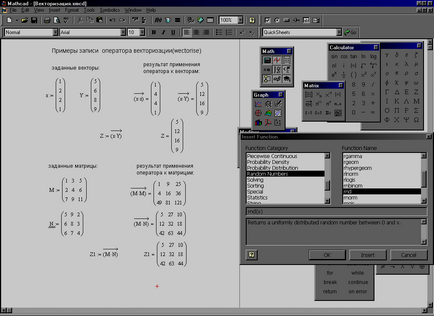
Fig. 3.13. Exemple de înregistrare a operatorului de vectorizare.
Introducerea operatorului elimină controversa asociată cu produsul scalar al vectorilor. Esența acestei contradicții este după cum urmează. Dacă, de exemplu, un vector este multiplicat cu produsul scalar al numărului, se transformă un nou vector, dintre care fiecare element este multiplicat cu acest număr, dar dacă scalarul este multiplicat cu același vector pentru sine, rezultatul este un număr egal cu suma pătratelor elementelor vectoriale, nu un vector.
operatorul vectorizare, în contrast cu produsul scalar, inmulteste fiecare vk element de (k = 1 ... n) al vectorului V prin elementul cu același număr (același indice) al unui alt sau același vector, producând un nou vector de aceeași lungime n.
Puteți introduce operatorul vectorize în două moduri:
- tastați Ctrl - (minus) "primul nume de operand" [Shift] * "al doilea nume de operand" = (egal) și faceți clic pe butonul stâng al mouse-ului;
- Faceți clic pe opțiunea "f (M)" de pe Matrix Matrix Panel și urmați aceeași procedură ca mai sus.
Operatorii operatorului de vectorizare pot fi matrici de aceeași dimensiune. De exemplu, dacă imprimare M * M [lacuna] [Ctrl] - (minus) = (egal), atunci vom obține o nouă matrice pătrată de aceeași dimensiune, ale cărei elemente sunt egale cu produsul fiecărui element al matricei M pentru sine.
Notă: Numărul de operanzi dintr-un operator vectorizat poate fi oricare, nu neapărat egal cu două.