In Fig.8, având în vedere proiecția ortogonală a punctului A arătat în cele două planuri perpendiculare reciproc de proiecție. Același desen prezintă planul imaginii de proiecție K, perpendicular pe planul orizontal H al proiecțiilor definite de urme sale k-k, și un punct de proiecție S. Proiecția centrală a punctului A poate fi obținut. ca puncte de intersecție a razelor de vedere trase din punctul de vedere prin punctul A și baza sa, cu un plan de imagine K.
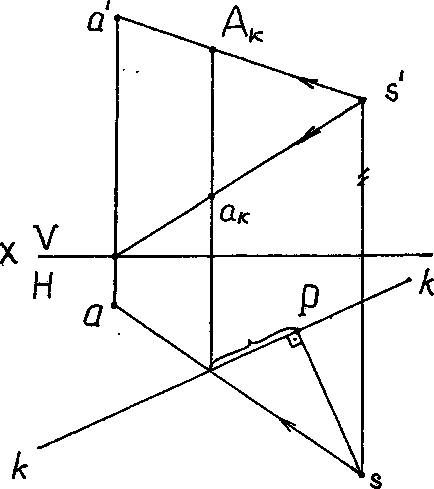
Fig. 8. Proiecțiile ortogonale sunt subțiri și sisteme de coordonate de perspectivă
În Fig. 9 prezintă, specificate separat planul imagine R, cu construit pe acesta un punct de vedere A. Poziția proiecției centrale a punctului A în raport cu modelul de bază definită printr-o proeminență frontală în Fig.8. Poziția legătură este identificată în raport cu punctul principal al imaginii - P. perspectivă linie dreaptă ortogonală pentru a specifica proiectat poate fi determinată cu privire la perspectivele pentru cele două puncte ale sale - toată lungimea așa cum se arată în Fig.8.
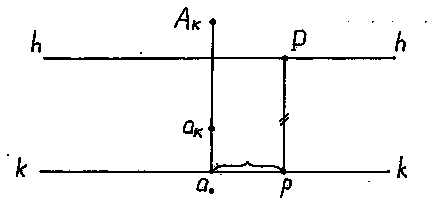
Fig. 9. Perspectiva unui punct construit din proiecțiile sale ortogonale
Perspectiva unui fascicul de linii drepte paralele. Punct de coborâre
Luați în considerare pe aparatul proiectat construcția proeminențelor centrale ale unui grup de linii drepte paralele situate în planul obiectului și în afara acestuia. Perspectiva fiecărei linii date este definită în desen prin următoarea imagine și punct limită. Pentru construirea punctelor limită, razele proeminente erau paralele cu direcția liniilor drepte și direcția bazelor lor. Din construcție rezultă că perspectivele liniilor au un punct limită comun F∞k. În consecință, grupul considerat de linii paralele este reprezentat în imagine sub forma unui pachet de linii care converg la un punct. Acest punct limită comun F∞k este numit punctul descendent al liniilor paralele, Fig.10,11.
Deoarece liniile paralele pot ocupa o poziție diferită în raport cu subiectul și planul imaginii, punctul de coborâre a proiecțiilor lor perspectivă va ocupa, de asemenea, o poziție diferită în raport cu principalele elemente ale imaginii - linia orizontului, principalul punct și astfel să stabilească amplasarea unui punct de perspective direcții cele mai caracteristice imagine de dispariție .. paralele drepte, Fig.10. 17.
Pentru a construi perspectivele liniilor drepte perpendiculare pe imagine, din punct de vedere S tragem o rază paralelă cu liniile date (figura 12). El va traversa planul imaginii în punctul principal al imaginii. În consecință, punctul principal al imaginii servește ca punct de plecare a perspectivelor liniilor drepte perpendiculare pe planul imaginii.
Este interesant de remarcat că liniile uneia sau altei imagini îndreptate către punctul său principal par să vină întotdeauna la spectator, din orice parte a imaginii.
Atunci când construim și citim imagini în perspectivă, este important să determinăm punctele de convergență a perspectivelor bazelor liniilor paralele date. În linii drepte perpendiculare pe planul imaginii, bazele lor sunt perpendiculare pe imagine ca și ele. Prin urmare, punctul principal al imaginii lui P, Ris-13
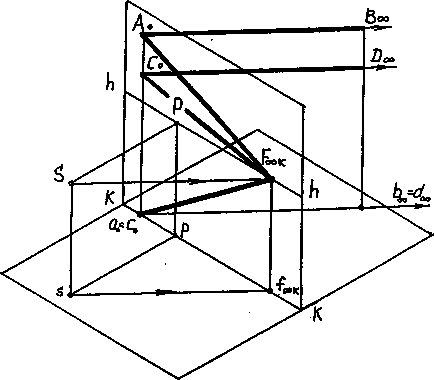
Fig. 10. Construcția unui punct de convergență al unui grup de linii drepte paralele
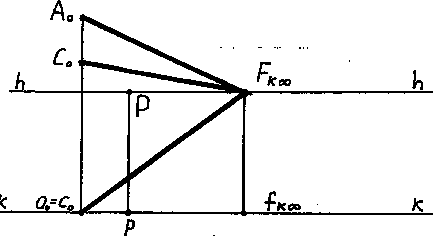
Figura 11. Perspectiva unui fascicul paralel
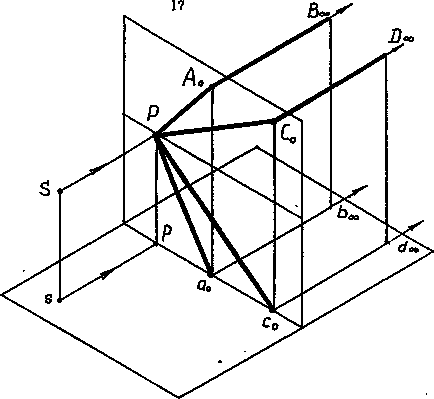
Fig. 12. Construirea perspectivei liniilor perpendiculare pe imagine
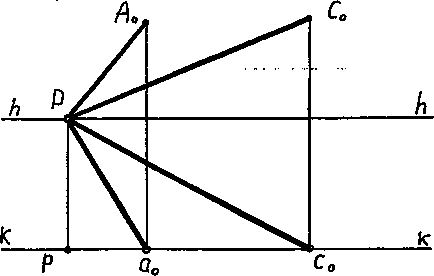
Fig. 13. Perspectiva liniilor drepte perpendiculare pe imagine
Când construim perspectivele celor mai diverse obiecte, aproape întotdeauna trebuie să ne confruntăm cu imaginea liniilor drepte situate în planurile orizontale și înclinate spre imagine în diferite unghiuri. Liniile drepte (fig.14), care sunt paralele cu planul obiectului, trebuie să fie poziționate și înclinate spre planul imaginii la un unghi de 45 °. Din punctul de vedere S tragem razele proeminente paralele cu liniile drepte date. Punctul de coborâre a liniilor drepte - Д1 va fi situat pe linia orizontului, t. Razele proeminente paralele cu liniile orizontale se află în planul orizontului. Segmentele DR și SP sunt egale unul cu celălalt ca părți ale unui triunghi SDS triunghi drept. Prin urmare, punctul obținut de coborâre D1 a coincis cu punctul de distanță al imaginii.
Astfel, unul dintre punctele de la distanță a lui D1 este punctul de coborâre a liniilor drepte orizontale care formează un unghi de 45 ° cu imaginea. A2 - Fig. 14. 15.
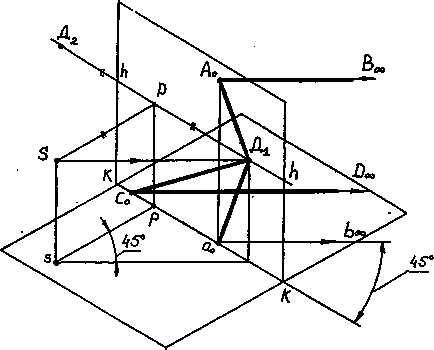
Figura 14. Construcția perspectivei liniilor orizontale drepte
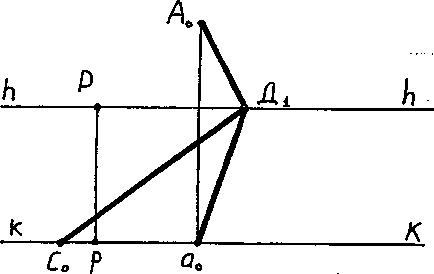
Figura 15. Perspectiva liniilor orizontale drepte
În cazul în care liniile orizontale sunt înclinate spre planul cerului la orice alte unghiuri, altele decât cele drepte și 45, este evident că punctul de fugă al acestor linii, deoarece nu va fi întotdeauna situat pe linia de orizont. Deoarece liniile orizontale sunt paralele cu planul obiectului, ele vor fi paralele cu bazele lor. Prin urmare, perspectivele pentru fundamentarea acestor linii directe vor fi îndreptate spre punctul de plecare al perspectivelor lor, Fig. 10. Fig. 11.
Ultimul caz de aranjare a liniilor orizontale este cel mai des întâlnit și se numește perspectivă unghiulară. O imagine de perspectivă bazată pe linii drepte perpendiculare pe imagine este numită perspectiva frontală.
Toate liniile drepte paralele cu planul imaginii pot fi împărțite în trei tipuri: linii drepte verticale; Straight, înclinat la planul obiectului; și linii drepte paralele cu planul obiectului. Evident, toate aceste linii nu vor avea o pistă de imagine. Pentru a construi o proiecție perspectivă a unui punct infinit de îndepărtat al liniilor în cauză, în paralel cu ele tragem din punct de vedere o rază proeminentă, Fig. 16. Apoi liniile verticale sunt prezentate în imagine ca pe verticală. Iar perspectivele pentru linii directe paralele cu imaginea vor fi paralele cu liniile drepte, Fig. 17.
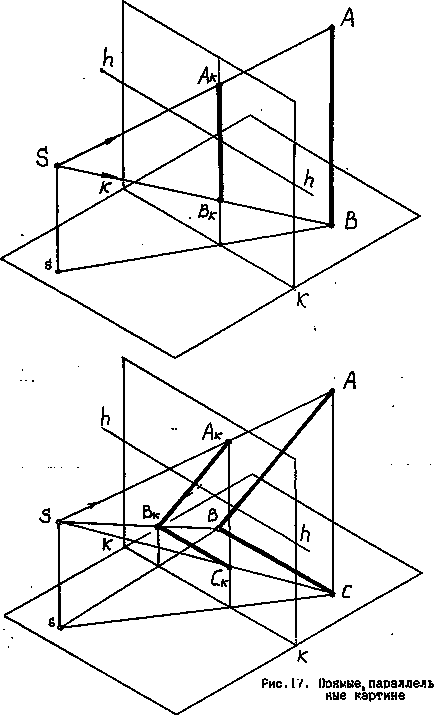
În partea superioară - Fig. 16 Vertical drept