
Acasă | Despre noi | feedback-ul
3.15. Pentru a asigura funcționarea normală a unei perechi de angrenaje cu un raport constant de transmisie, profilele dintelui trebuie să fie delimitate
Pe curbe supuse anumitor legi. Aceste legi rezultă din teorema principală a legăturii, esența căreia constă în următoarele.
Să existe o pereche de roți dințate cu centrele O1 și O2 care se rotesc: în mod corespunzător cu vitezele unghiulare ω și ω2. În Fig. 3.18, a arată adaosul, care ocupă în mod consecvent o pereche de dinți conjugați (involunți) în timpul angajării lor; linia dreaptă O1 O2 este numită linia interaxică a trenului de viteze. Tragem în punctele de contact ale dinților K1. K2,
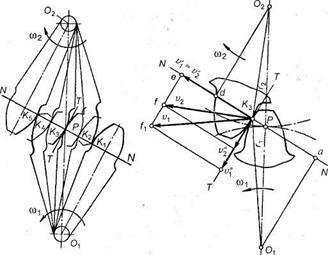
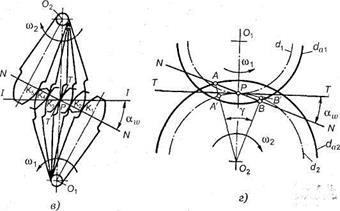
Fig. 3.18. Elemente de angrenare
Kg. normale generale la profile. Toate aceste normale NN trebuie să intersecteze linia centrală O1 O2 la un punct constant P. Acest punct este numit polul de legătură; poziția sa pe linia interaxiană este determinată de raportul dintre vitezele unghiulare ale roților, adică raportul lor:
Vrac Teorema angajament poate fi formulată după cum urmează: totală nor-mal la profilurile dinților la punctul lor de contact intersectează linia interaxiala la punctul P, numit pol segmente de distanțiere de îmbinare și de divizare nu invers proporțională cu viteza unghiulară.
Corolar: pentru a asigura un raport constant de transmisie, poziția polului P pe linia centrală trebuie să fie constantă.
3.16. În timpul funcționării profilelor conjugate (evoluează), punctul lor de contact se mișcă continuu de-a lungul liniei NN. Această linie dreaptă se numește linia de legătură.
Locul (punctul) de încurcare și ieșire din dinții conjugați poate fi determinat prin următoarea construcție geometrică.
Luăm o distanță interactivă arbitrară O1 O2 (Figura 3.18, d) și o împărțim într-un raport arbitrar O2 P / O1 P = u. Raze F O2 O1 P și trage angrenajelor circumferința inițială prin punctul P, tangenta TT-ing la aceste cercuri și linia NN - normală la suprafața marginii styam dinților - un unghi a # 969; și tangenta TT. Unghiul un # 969; numit unghiul de atașament; în CSI a # 969, adoptată 20 °.
Luăm o înălțime arbitrară a capului dentar și o tragem cu raze. egală cu 1 / 2da1 și 1 / 2da2, pinioane proeminențe circumferențiale (înălțimea pinioanele și roțile dinte agil trebuie sa fie la fel). În cazul în care direcția de rotație a roții este prezentat în figură, dinții vin în angrenare la punctul A (punctul de intersecție cu circumferința normală a proeminențelor roților) se va stinge: din angajament la punctul B (punctul de intersecție cu circumferința proeminențelor dințate normale).
Toate punctele de contact ale dinților conjugați se află pe secțiunea AB a liniei de legătură. Secțiunea AB este denumită secțiunea de lucru a liniei de legătură.
O condiție necesară pentru continuitatea legăturii: arcul de legătură trebuie să fie mai mare decât pasul. În caz contrar, dacă o pereche de dinți se detașează de angajament, a doua pereche nu intră încă.
Lungimea liniei de cuplare qa este un segment al liniei de cuplare, tăiat: prin circumferințele vârfurilor dinților roților conjugate. Aceasta determină începutul y. capătul de cuplare a unei perechi de dinți conjugați. Lungimea ochiului este partea activă a liniei de plasă.
Coeficient de suprapunere a feței A - raportul dintre lungimea liniei de atașare și pasul:
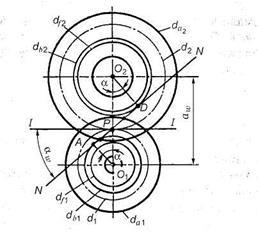
Fig. 3,19. Parametrii geometrici ai trenului de viteze
Este posibil să vedeți pe roata dințată (Figura 3.19) linia de cuplare NN și unghiul de angajare aw sau este doar elementele geometrice reprezentate teoretic?
Polul legăturii P (a se vedea figura 3.18, b) păstrează poziția neschimbată pe linia de centru 01 02. Prin urmare, razele 01 P (r1) și 02 P (r2) sunt, de asemenea, neschimbate. Cercurile de radii r1 și r2 se numesc inițiale (divizibile - vezi pasul 3.13). Atunci când uneltele se rotesc, aceste cercuri sunt traversate unul după altul fără alunecare, după cum rezultă din egalitatea vitezelor lor circumferențiale # 969; 1 r1 = 2 r2 (a se vedea dovada teoriei principale a legăturii). Teoretic, suprafețele laterale ale dinților (profilare) pot fi subliniate de orice curbe care satisfac legea de bază a angrenajului. Astfel de profiluri se numesc conjugate.
În ingineria modernă, un număr limitat de curbe sunt folosite pentru a construi profile conjugate.