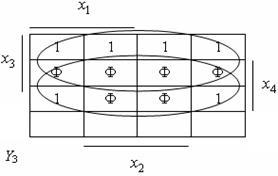
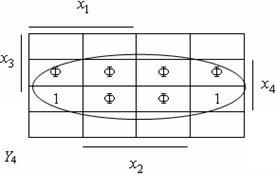
Fig. 4.1. Carnot Codul convertorului Carnot
O diagramă bazată pe aceste formule structurale în baza N-HE este prezentată în Fig. 4.2.
Fig. 4.2. Schema bloc a convertorului de coduri
Codificatoare - convertoarele codului de poziție într-un cod binar, adică conversia semnalului 1 pe una dintre intrările în codul corespunzător de pe magistralele de ieșire. Dacă ieșirea este cod m-bit, atunci numărul maxim de intrări este n = 2 m. Dacă sunt folosite toate intrările de 2 m, atunci acest codificator este numit complet, dacă nu tot, apoi incomplet. Funcționarea codificatorului 4 2 este reprezentată de un tabel de adevăr (Tabelul 4.2). Din tabelă rezultă:
adică, pentru a construi un astfel de codificator, două LE OR sunt necesare pentru două intrări.
De asemenea, codificatorii sunt construiți pentru un număr mai mare de cifre.
Dezavantajul acestor encodere este ambiguitatea, dacă mai multe intrări sunt inițiate simultan. Pentru ca encoder-ul să răspundă doar la o intrare excitat, sunt construiți codificatoare prioritare. În ele, în cazul excitării simultane a mai multor intrări, codul de ieșire va corespunde numărului "senior" ("inferior") de la intrările excitate. În Fig. 4.3 arată desemnarea unui astfel de codificator. Encoderul prioritar are concluzii suplimentare: E1 - semnal de activare a codorului, E0 - semnal despre absența intrărilor excitate, G - semnal de ieșire indicând cel puțin o intrare excitat.
Prezența concluziilor E1. E0, G vă permite să măriți numărul de codificatoare.
Decodorul este un convertor al codului binar n-bit într-un cod unitar de 2 n-cifre, adică decodorul are n intrări și m = 2 n ieșiri. Fiecare set de variabile de intrare corespunde excitației (apariția unei unități logice sau zero) la ieșire, numărul zecimal care corespunde codului binar.
Să luăm în considerare un exemplu de construire a unui decodificator cu două cifre. Funcția decodorului poate fi reprezentată de o tabelă de adevăr (Tabelul 4.3) Din tabel, obținem expresii pentru funcțiile de ieșire (Y1) ale decodorului:
Din relațiile obținute este evident că pentru construirea decodorului sunt necesare patru elemente logice AND pentru două intrări și două invertoare. Deseori, decodoarele sunt construite în baza NAND (vezi Figura 4.4). În acest caz, ieșirile vor fi inverse, adică ieșirea corespunde unei logici zero; și pentru a obține o ieșire directă, aveți nevoie de încă patru invertoare. Pentru a extinde capabilitățile decodorului în circuitele integrate, încă o intrare este făcută cu rezoluție E. Pentru organizarea sa, elementele AND-N sunt luate la 3 intrări - cele trei intrări sunt combinate și formează intrarea rezoluției. În acest caz, decodorul funcționează când există o unitate logică pe intrarea E.
Fig. 4.4. Structura decodorului
O reprezentare grafică a decodoarelor este prezentată în Fig. 4.5. Dacă ieșirile sunt inverse, atunci ele sunt notate cu cercuri.
Prezența unei intrări de rezoluție permite creșterea adâncimii bitului decodorului. În Fig. 4.6 arată cum se construiește un decodor de trei cifre utilizând decodoare pe două biți.
Fig. 4.6. Extinderea decodoarelor
Pentru toate seturile de variabile de intrare, unde x3 = 0, DC2 va funcționa, deoarece o unitate va ajunge la intrarea lui E2. Atunci când x3 = 1, decodorul DC3 funcționează corespunzător, astfel obținându-se trei intrări și opt ieșiri. Pentru a extinde numărul de intrări și ieșiri, puteți utiliza un decodor paralel (dreptunghiular), dar pentru aceasta, pe lângă decodoare, aveți nevoie de elemente 2I.
Folosind decodoare și elemente logice suplimentare, puteți implementa aproape orice funcție logică.
Luați în considerare acest exemplu
Tabelul de adevăr pentru această funcție este fila. 4.4. Pentru ao implementa, aveți nevoie de un decodor 2 4 și o poartă OR la două intrări (Figura 4.7). Atunci când x1 sau x2 sunt egale cu unul (pentru un set de n = 1 și n = 2), unul apare la ieșirile decodorului (1 sau 2), iar funcția de ieșire este 1.
Fig. 4.7. Diagrama bloc a agregatului
modulo 2 de pe decodor
Funcționarea multiplexorului pe două biți este reprezentată de un tabel de adevăr (Tabelul 4.5). Funcționarea multiplexorului este descrisă printr-o ecuație logică
În conformitate cu ecuația de construire a unui multiplexor, sunt necesare un element 3I-4I și două invertoare. Schema bloc este prezentată în Fig. 4.8, o reprezentare grafică a multiplexorilor este prezentată în Fig. 4.9.
Fig. 4.7. Schema bloc a multiplexorului
Fig. 4.9 Simbol pentru multiplexoare
Fig. 4.10. Schema de multiplexare
Fig. 4.12. Imagine condiționată
demultiplexor
Trebuie remarcat faptul că multiplexoarele și demultiplexoarele în serie pe tranzistoare bipolare comută numai semnale digitale, adică 0 sau 1.
Fig. 4.12. Schema funcțională a multiplexorului-demultiplexor
Un adder este un circuit combinațional conceput pentru a adăuga numere binare. Cea mai simplă sarcină este să adăugați două numere de o singură cifră. Pentru a dezvolta o schemă logică, trebuie luate în considerare în primul rând toate combinațiile posibile de variabile de intrare, pe baza cărora se poate face o tabelă de stări. La adăugarea numerelor de o singură cifră A și B, se pot observa următoarele combinații:
adică dacă A = B = 1, transferul are loc la următoarea (mai veche) cifră. Prin urmare, un astfel de sumator trebuie să aibă două ieșiri: unul pentru formarea părții din suma aparținând cifrei date, iar al doilea pentru transferul la următoarea cifră. Reprezentarea numerelor și a variabilelor logice a0. B0. compilam o tabelă de stări (Tabelul 4.8), unde S0 este suma, P este semnalul de transfer.
Prin urmare, compilam ecuațiile logice în SDNF:
și să construiască diagramele structurale (Figura 4.14, Figura 4.15).
Fig. 4.14. Totalizer modulo două Fig. 4.15. Schema de transfer
Circuitul care realizează ecuația 1 se numește OR exclusiv, este lansat în serie ca un cip separat. Denumirea grafică este prezentată în figura 4.16. Operația logică efectuată de acest circuit este
unde este simbolul de însumare modulo doi.