Astăzi vom vorbi despre un subiect care excită toți elevii din clasele 8-9 când încep să studieze trigonometria adultă gravă. Vorbim despre măsura radianului unghiului și despre transferul de la radian la măsura gradului unghiului și a spatelui. Dar, înainte de a începe să rezolve unele probleme cu privire la calculul măsurii radian, aș dori să amintesc vechea definiție a ceea ce sinus, cosinus și tangenta unui unghi într-un triunghi dreptunghic.
Un pic de teorie
Să desenăm un triunghi dreptunghiular, să-l sunăm
și C C va fi direct:
Unghiul A A este egal cu gradele α \ alpha. În acest caz, după cum vă amintiți din cursul de școală al geometriei, sinusul, cosinusul și tangenta vor fi aceleași:
După cum puteți vedea, definiția clasică a sinus, cosinus, tangentă și cotangentă este fixat într-un triunghi dreptunghic, și α \ alfa, în orice caz, ar trebui să fie mai mare decât 0º și mai puțin de 90 de grade.
În ciuda acestui fapt, a devenit necesară extinderea definiției funcțiilor trigonometrice dincolo de acest interval de la 0 ° la 90 °. Cum se întâmplă acest lucru și ce fel de efecte aveți? Acum, să vorbim despre asta.
Mai întâi, să luăm în considerare planul de coordonate: tragem axele x x, y y și construim un cerc unic cu centrul de la origine:
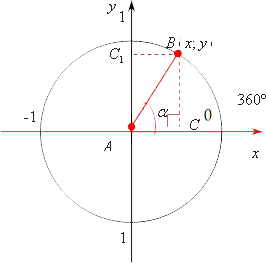
O mică clarificare în terminologie, ce înseamnă cercul unic? Este foarte simplu. Aceasta înseamnă că raza sa este strict 1. Cu alte cuvinte, ea trece prin punctul (1; 0) și de asemenea (0; 1). Și prin celelalte două puncte trece și acest cerc. Acum trebuie să pornim de la originea razei de-a lungul axei Ox Ox. Aceasta este direcția pozitivă a axei Ox Ox. Apoi notăm α \ alpha în direcția x x la y y. Desigur, această rază va traversa cercul nostru într-o anumită valoare, să o denotăm prin punctul B. Noi denotăm originea cu punctul A A. Desenați de la B B înălțimea la axa absciselor x x. Obținem C C. Aici avem din nou același triunghi dreptunghiular ABC ABC cu unghi α \ alpha. a cărui vârf coincide cu originea.
Ce este sinusoidal?
Acum, să rescriem sinele, cosinusul și tangenta, luând în considerare toate modificările pentru triunghiul roșu. Noi scriem:
Totuși. Cu toate acestea, rețineți că B B nu se află într-un spațiu vag, are anumite coordonate, deoarece se află în planul Oxy Oxy. Fie coordonatele sale (x, y) \ left (x; y \ right). Nu știm exact la ce sunt egali, deoarece nu cunoaștem unghiul a \ alpha. .. În acest caz, lungimea segmentului BC BCravnyaetsya yy, respectiv ordonata punctului B B. In schimb BC BC putem scrie yy, dar în loc de AB AB - 1. AB AB - aceasta este aceeași rază a cercului nostru, iar raza - 1. Scrie :
sinα = BC AB = y r = y
Astfel, putem scrie că sinα \ sin \ alpha este de fapt egal cu ordinea sfârșitului razei mobile. Aceasta este expresia cea mai des întâlnită de studenți în manualele școlare de matematică. Prin urmare, înainte de a merge mai departe, să aruncăm o privire mai departe la triunghiul ABC ABC și, în special, la B B.
Am ținut încă o înălțime, o numim B C 1 B_>. Ce puteți spune despre C 1 _>, sau mai precis, despre lungimea AC 1 A_> - este coordonata y B B. Pe de altă parte, intervalul de curent alternativ AC, adică distanța de la AA la CC - .. Este coordonatele punctului de xx CC și în consecință , xx a punctului B B. Se va dovedi ușor că segmentele BC BC și AC 1 A_> sunt egale. Apoi putem afirma că segmentul AB AB este, de asemenea, y y. Deci, am sortat sinusoidele. Într-adevăr, sinusul unghiului α \ alpha ordonata este sfârșitul intervalului mobil, a avut loc la punctul B B. Acum să scrie aceeași expresie pentru cosinusul și tangenta.
Ce este cosinusul?
Această relație a picioarelor adiacente (în cazul nostru este AC AC) la hypotenuse (avem AB AB). Dar ce este AC AC? Tocmai am văzut că AC AC este abscisa, adică coordonata x x. AB AB are aceeași rază, adică 1. Scrieți:
cosá = AC AB = x r = x
Ce este o tangenta?
Acum să aruncăm o privire la tg α tg \ alpha. Este încă mai ușor. Ce este o tangenta? Acest raport al piciorului opus (în cazul nostru este BC BC) la piciorul adiacent (în cazul nostru este AC AC). Noi scriem:
tg α = BC AC = y x
Astfel, tg tg este raportul dintre ordonată și abscisa de la sfârșitul razei mobile.
Și în acel moment, mulți studenți vor întreba probabil: "Dar de ce toată această complexitate?". În acest caz, atunci când B B este pur și simplu dat de intersecția razei cu cercul, putem amâna orice unghi α \ alpha. Acum nu există restricții privind desemnarea α \ alpha. Nu trebuie să fie un unghi între 0 ° și 90 °.
Calcularea mărimii radianului unghiului
Acum, că ne-am ocupat de definițiile de bază ale funcțiilor trigonometrice, să ne îndreptăm direct către subiectul actual al lecției.
În primul rând, să examinăm un unghi de 180 °. Atunci fasciculul nostru se potrivește în direcția opusă. Punctul B din triunghiul nostru sculptează un anumit arc al cercului. Noi numim arcul BC BC. Este ușor de calculat prin formula lungimii cercului:
\ pi \ tilde3,14. Dar acum nu ne interesează. Deoarece cercul nostru are întotdeauna o rază fixă de 1, lungimea va fi:
Cu toate acestea, 2π 2 \ pi este cercul întreg, adică revoluția completă. Și dacă ne retragem la 180 de grade, vom primi doar jumătate din ea. Prin urmare, arcul cercului va fi egal cu:
l (180 o) = 2 π 2 = π
l \ stânga (180<>^ \ text \ right) = \ frac = \ pi
Și aici există un efect remarcabil. Faptul că unul și același unghi α \ alfa putem desemna atât de 180º, t. E. Utilizați măsura standard de unghi (și nu radian), si lung e acest arc, adică. E., Putem furniza unghi alfa \ alpha este numărul corespunzător π \ pi. Deci, acesta este numărul π \ pi. cu alte cuvinte, unghiul nu este măsurat în grade, ci în lungimea arcului pe care-l sculptează acest colț. Aceasta se numește măsura radianului unghiului și este desemnată π \ pi - radian.
Astăzi, pentru a începe rezolvarea problemelor cu privire la măsura radianului și luați în considerare valoarea funcțiilor trigonometrice, amintiți-vă doar că π \ pi rad = 180º. Cu alte cuvinte, dacă nu sunteți obișnuit să lucrați cu valori radiane, atunci oriunde vedeți în sines, cosines și tangenți construirea lui pi. puteți înlocui în siguranță acest p cu 180 ° și mergeți la gradul familiar de la măsura radianului. Să încercăm să calculam prima expresie și să găsim măsura radianului:
Să scriem separat fiecare dintre aceste funcții:
sin sin 4 = sin 180 ∘ 4 = sin45 ∘ = 2 √ 2 \ sin \ frac \! \! \ pi \! \! \ text<>> = \ sin \ frac ^ \ circ> = \ sin 45<>^ \ circ = \ frac>
cos π 6 = cos 180 ∘ 6 = cos30 ∘ = 3 √ 2 \ cos \ frac \! \! \ pi \! \! \ text<>> = \ cos \ frac ^ \ circ> = \ cos 30<>^ \ circ = \ frac>
tg π 3 = tg 180 ∘ 3 = tg 60 ∘ = 3 √ tg \ frac \! \! \ pi \! \! \ text<>> = tg \ frac ^ \ circ> = tg60<>^ \ circ = \ sqrt
Acum scrieți toți cei trei factori într-o singură construcție pentru a găsi valoarea radianului. Asta e tot, am primit răspunsul.
Trecem la a doua expresie și găsim măsura radianului:
Din nou, scrieți fiecare funcție separat:
cos π 3 = cos60 ∘ = 1 2 \ cos \ frac \! \! \ pi \! \! \ text<>> = \ cos 60<>^ \ circ = \ frac
ctg π 6 = ctg 30 ∘ = 3 √ ctg \ frac = ctg30<>^ \ circ = \ sqrt
Din nou, colectăm toate numerele obținute.
După cum puteți vedea, nimic nu este complicat în măsura radianului unghiului. Dacă acest subiect pare prea complicat pentru dvs., trebuie doar să vă amintiți că π \ pi rad = 180º și oriunde vedeți p \ pi. se poate scrie în siguranță cu 180 °.
O altă consecință importantă a noii definiții a cercului trigonometric este aceea că sinus, cosinus și tangent pot fi negative. Dacă mai devreme totul se fierbe până la lungimea picioarelor și a hypotenusei, acum avem abscise și ordonate ale unui anumit punct. Amintiți-vă, totuși, că așezarea unghiului merge întotdeauna în direcția de la axa Ox Ox până la axa Oy Oy și tocmai direcțiile pozitive ale acestor axe.
Pentru a înțelege și a ne aminti pentru totdeauna unde este direcția axei pozitive, amintiți-vă doar regula: unde săgețile indică la x și la y, aceasta este direcția cea mai pozitivă a axei.
- Pregătirea gratuită pentru USE 7 lecții simple, dar foarte utile + temele
