Conceptul de mișcare browniană
Legile mișcării browniene și aplicarea în știință
Conceptul de mișcare browniană din punctul de vedere al teoriei haosului
Mișcarea mingii de biliard
Integrarea fracturilor deterministe și a haosului
Conceptul de mișcare browniană
mișcare browniană corect mișcarea browniană, particulele de substanță mișcare termică (dimensiunea mai multor microni sau mai puțin), sunt suspendate în particulele de lichid sau gaz. mișcarea browniană este cauza unui număr de impulsuri necompensate, care sunt primite de particula browniană de moleculele din jur într-un lichid sau gaz. Deschis P. Browne (1773 - 1858) în 1827. vizibil numai sub microscop suspendate particulele se mișcă independent și să descrie traiectoria complexă în zig-zag. Miscarea Brownian nu slăbește cu timpul și nu depinde de proprietățile chimice ale mediului. Intensitatea mișcării Brownian crește odată cu creșterea temperaturii mediului și cu scăderea vâscozității și dimensiunilor particulelor.
O explicație secvențială a mișcării browniene a fost dată de A. Einstein și M. Smoluchowski în 1905-06 pe baza teoriei moleculare-cinetice. Conform acestei teorii, moleculele unui lichid sau gaz sunt în mișcare termică constantă, iar impulsurile diferitelor molecule nu sunt aceleași în mărime și direcție. Dacă suprafața unei particule plasată într-un astfel de mediu este mică, cum este cazul unei particule browniene, atunci impactul cu care se confruntă particula din moleculele care o înconjoară nu va fi exact compensată. Prin urmare, ca rezultat al "bombardamentului" de către molecule, particula bruniană intră în mișcare dezordonată, schimbând magnitudinea și direcția vitezei sale de aproximativ 10 14 ori pe secundă. Când se observă mișcarea Brownian, poziția particulei este fixată (vezi figura 1) la intervale regulate. Desigur, între observații particula nu se mișcă rectiliniu, dar legătura pozițiilor succesive cu linii drepte dă o imagine condiționată a mișcării.
Aflarea bruscă a unei particule de gummogut în apă (figura 1)
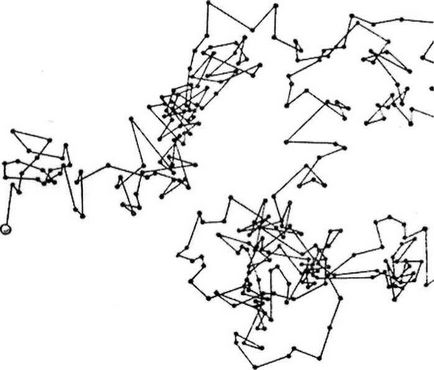
Legile mișcării Browniene
Legile mișcării browniene servesc ca o confirmare clară a pozițiilor fundamentale ale teoriei moleculare-cinetice. Imaginea generală a mișcării browniene este descrisă de legea lui Einstein pentru pătratul mediu al deplasării particulei de-a lungul oricărei direcții x. Dacă într-un interval de timp între două măsurători se produce un număr suficient de mare de coliziuni ale unei particule cu molecule, atunci este proporțională cu acest timp t:
Aici D este coeficientul de difuzie, care este determinat de rezistența exercitată de mediul vâscos al unei particule care se mișcă în ea. Pentru particule sferice de rază și este egal cu:
unde k este constanta Boltzmann, T este temperatura absolută și h este vâscozitatea dinamică a mediului. Teoria mișcării browniene explică mișcarea aleatorie a unei particule prin acțiunea forțelor aleatorii din partea moleculelor și a forțelor de fricțiune. Natura aleatoare a forței înseamnă că acțiunea ei pe un interval de timp t 1 este complet independentă de acțiune pe intervalul t 2. Dacă aceste intervale nu se suprapun. Forța într-un timp suficient de mare este zero, iar deplasarea medie a particulei Brownian se dovedește, de asemenea, zero. Concluziile teoriei mișcării browniene sunt de acord cu experimentul, formulele (1) și (2) au fost confirmate prin măsurătorile lui J. Perrin și T. Svedberg (1906). Pe baza acestor relații, constantele Boltzmann și Avogadro au fost determinate experimental în concordanță cu valorile obținute prin alte metode. Teoria mișcării browniene a jucat un rol important în fundamentarea mecanicii statistice. În plus, are o valoare practică. În primul rând, mișcarea Brownian limitează acuratețea instrumentelor de măsurare. De exemplu, limita de precizie a citirilor unui galvanometru oglindă este determinată de tremuratul unei oglinzi, ca o particulă bruniană bombardată de moleculele de aer. Legile mișcării Brownian determină mișcarea aleatorie a electronilor, ceea ce provoacă zgomot în circuitele electrice. Pierderile dielectrice în dielectric sunt explicate prin mișcarea aleatorie a moleculelor dipol care alcătuiesc dielectricul. Mișcarea aleatorie a ionilor în soluțiile de electroliți mărește rezistența lor electrică.
Conceptul de mișcare browniană din punctul de vedere al teoriei haosului

Miscarea browniană este, de exemplu, mișcarea aleatorie și haotică a particulelor de praf suspendate în apă. Acest tip de mișcare, poate, este un aspect al geometriei fractale, având cea mai practică utilizare. Mișcarea Brownian aleatorie produce o diagrama de frecvențe care poate fi utilizată pentru a prezice lucruri care implică cantități mari de date și statistici. Un bun exemplu sunt prețurile la lână, pe care Mandelbrot le-a prezis cu ajutorul mișcării browniene.

Diagramele de frecvență create atunci când se compilează o diagramă bazată pe numere Brownian pot fi, de asemenea, convertite în muzică. Desigur, acest tip de muzică fractală nu este deloc muzical și poate purta cu adevărat ascultătorul.
Prin plotarea numerelor Brownian aleatoare pe o diagramă, puteți obține Dust Fractal similar cu ceea ce este dat aici ca un exemplu. Pe lângă aplicarea mișcării Brownian pentru a obține fractalii fractali, ea poate fi folosită și pentru a crea peisaje. În multe filme fantastice, cum ar fi Star Trek, tehnica mișcării Brownian a fost folosită pentru a crea peisaje străine, cum ar fi dealuri și imagini topologice ale platourilor înalte.
Aceste tehnici sunt foarte eficiente și pot fi găsite în cartea lui Mandelbrot Fragmentarea geometriei naturii. Mandelbrot a folosit liniile Brownian pentru a crea linii de coastă fractale și hărți insulare (care, de fapt, au fost doar puncte aleatorii aleatoriu) din punctul de vedere al păsărilor.
BILIARD BALL MOVEMENT
Oricine a luat vreodată un indiciu pentru biliard știe că cheia jocului este acuratețea. Cea mai mică eroare în unghiul cursei inițiale poate duce rapid la o greșeală uriașă în poziția mingii după doar câteva coliziuni. Această sensibilitate la condițiile inițiale numit haos apare bariera de netrecut pentru oricine care speră să prezică sau să controleze traiectoria mișcării mingii după mai mult de șase sau șapte coliziuni. Și nu credeți că problema se află în praful de pe masă sau în mâna instabilă. De fapt, dacă utilizați computerul pentru construirea unui model care conține o masă de biliard, nu are nici frecări, control de precizie inumană de poziționare a tac, tot nu va fi capabil de a prezice traiectoria mingii pentru o lungă perioadă de timp!

Cât timp? Aceasta depinde în parte de precizia calculatorului dvs., dar mai mult pe forma mesei. Pentru o masă rotundă perfectă, este posibil să se calculeze până la aproximativ 500 de locații de coliziune cu o eroare de aproximativ 0,1%. Dar merită schimbarea formei mesei astfel încât să devină cel puțin puțin neregulată (ovală), iar imprevizibilitatea traiectoriei poate depăși 90 de grade după 10 coliziuni! Singura modalitate de a obŃine o imagine a comportamentului general al unei bile de biliard care cade pe o masă curată este reprezentarea unghiului de săritură sau a lungimii arcului care corespunde fiecărei curse. Două magnificări consecutive ale unei astfel de imagini cu faza-spațiu sunt date aici.

Fiecare buclă individuală sau zona de împrăștiere a punctelor reprezintă comportamentul mingii, pornind de la un set de condiții inițiale. Zona imaginii, care afișează rezultatele unui experiment anume, se numește domeniul atractor pentru un anumit set de condiții inițiale. După cum se poate observa, forma mesei folosite pentru aceste experimente este partea principală a zonelor de atracție, care se repetă succesiv pe o scară descrescătoare. Teoretic, o astfel de auto-similitudine ar trebui să continue pentru totdeauna și, dacă vom crește din ce în ce mai mult cifra, vom primi toate aceleași forme. Acest lucru se numește astăzi foarte popular, cuvântul fractal.
INTEGRAREA FRACTALELOR DETERMINATE ȘI CHAOS
Din exemplele de fracturi deterministe, se poate observa că nu prezintă un comportament haotic și că sunt de fapt foarte previzibile. După cum se știe, teoria haosului folosește un fractal pentru a recrea sau a găsi modele pentru a prezice comportamentul multor sisteme în natură, cum ar fi, de exemplu, problema migrației păsărilor.
Acum, să vedem cum se întâmplă acest lucru cu adevărat. Folosind fractalul denumit Arborele lui Pitagora, nu este considerată aici (care, de altfel, nu este inventat de Pitagora, și nu are nimic de a face cu teorema lui Pitagora) și mișcarea browniană (care este haotică), să încercăm să facem o simulare a unui copac real. Rationalizarea frunze și ramuri de copac este dificil și din greșeală, și, probabil, nu este ceva destul de simplu, care poate emula un program scurt de 12 linii.
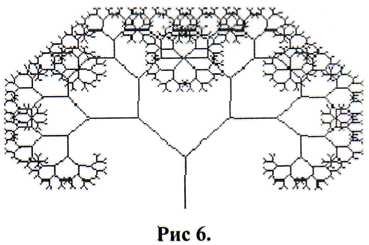
Mai întâi trebuie să generați arborele Pythagoras (stânga). Este necesar ca portbagajul să fie mai gros. În această etapă, mișcarea Brownian nu este folosită. În schimb, fiecare segment de linie devine acum linia de simetrie a dreptunghiului care devine trunchi, iar ramurile sunt în afara.
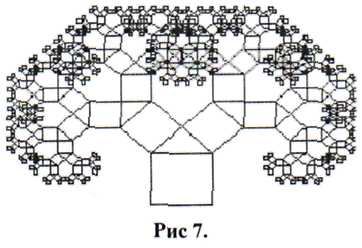
Dar rezultatul pare încă prea formal și ordonat. Arborele nu pare încă viu. Să încercăm să aplicăm o parte din aceste cunoștințe în domeniul fracturilor deterministe, pe care tocmai le-am dobândit.
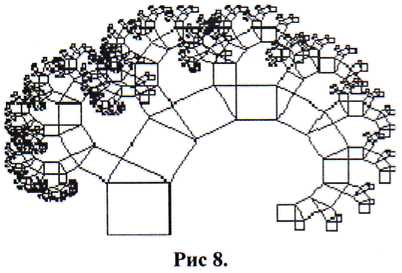
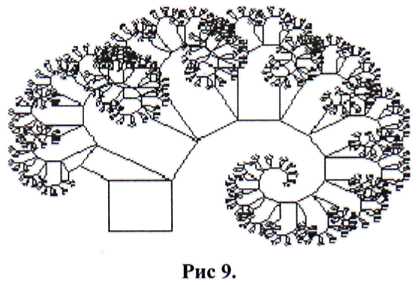
Acum puteți utiliza mișcarea Brownian pentru a crea o întâmplare aleatorie, care schimbă numerele, rotunjdu-le până la două cifre. În versiunea originală, s-au folosit numere zecimale pe 39 de biți. Rezultatul (pe partea stângă) nu arată ca un copac. În schimb, arata ca un cârlig de pește.
Poate că rotunjirea a 2 cifre a fost prea mare? Din nou, aplicăm mișcarea browniană, rotunjită de această dată cu până la 7 cifre. Rezultatul încă arată ca un cârlig de pescuit, dar de această dată sub forma unei spirale logaritmice!
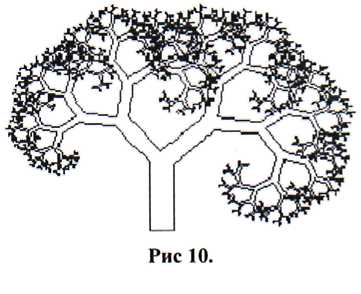
Deoarece partea stângă (care conține toate numerele impare) nu produce efectul de cârlig, aleatoria aleatoare produsă de mișcarea Brownian este aplicată de două ori la toate numerele din partea stângă și o singură dată la numerele din dreapta. Poate că acest lucru va fi suficient pentru a exclude sau a reduce efectul spiralei logaritmice. Deci, numerele sunt rotunjite până la 24 de cifre. De data aceasta, rezultatul este o emulație arborescentă arborescentă reală computerizată.
Arta similara:
Mișcarea ca mod de a fi
2 INTRODUCERE 3 1 CONCEPTUL "CIRCULAȚIE". MATERIAL ȘI RELAȚIA DE CIRCULAȚIE. PROBLEMA DE SURSĂ DE CIRCULAȚIE. TRAFIC ȘI REST 4 2 FORME DE BAZĂ. materie. Procesele care au loc în natură neînsuflețită (mișcare Browniană etc.), procese biologice (mutageneză, etc.).
Punct material. Organismul de referință. Sistemul de referință. Legea cinematică a mișcării materialului
teoriile și justificarea lor experimentală. Miscarea lui Brown. Masa și dimensiunea moleculelor. Miscarea Brownian este mișcarea continuă haotică a particulelor microscopice care sunt insolubile într-un lichid. Mișcarea particulelor Brown se explică printr-o mișcare haotică.
au sisteme microheterogene capabile să participe la mișcarea Browniană. în urma căruia particulele fazei dispersate. și energia cinetică a particulelor EK care participă la mișcarea browniană. Starea sistemului coloidal depinde de.
Curs de lucru >> Informatică
Aplicarea teoriei haosului în lumea reală 2.3.4 Mișcarea browniană și aplicarea ei 2.4 Integrarea fractalurilor deterministe. cunoștințe pentru ziua de azi. 2.3.4 Propunerea mișcării browniene și aplicarea acesteia Propunerea Brownian este, de exemplu, o întâmplătoare și.
în astfel de fenomene ca mișcarea Browniană. difuzie, presiune osmotică. Particulele. circulație. Astfel, mișcarea Brownian este o consecință a mișcării termice în mediul de dispersie și o reflectare directă a statisticilor. Miscarea lui Brown.