Fractalii din C ++ pentru ceainici densi.
"Traseul rusesc" în teoria fractalilor
Termenul "fractal" a fost introdus în matematicianul francez de origine poloneză Benoit Mandelbrot în 1975. În cartea sa "Geometria fractală a naturii" el scrie: "Un fractal este o structură formată din părți care într-un fel sunt similare cu întregul".

Un fractal poate fi un obiect cu structura "auto-asemănării". Un exemplu tipic - o jucărie rusă din lemn Matryoshka, în interiorul căreia există figuri similare de dimensiuni mai mici. Rusesc "fractal" pictat Matryoshka a apărut în Rusia la sfârșitul secolului XIX. Puțini oameni știu că Lefty nu numai că a împins puricii, ci a construit și o cuibărind dimensiunea unui puricător. Și Chubais lucrează în prezent la crearea unei păpuși nano-matryoshka. În curând va fi posibil să vorbim despre "urmă rusă" în teoria fractalilor!
În 1872, matematicianul german Karl Weierstrass a construit o funcție continuă sub forma unei serii trigonometrice infinite, care nu este niciodată diferențiată. Problema rezolvată de el încă tulbură întrebările insidioase ale elevilor din examenul de matematică: "Dacă funcția este continuă - este ea diferențiată?".
Doar pentru că voi clarifica. Dacă o curbă continuă are un punct de rupere, atunci în acest punct nu are o tangentă. O funcție a cărei grafică este această curbă nu poate fi diferențiată la punctul de rupere! Deci, graficul funcției Weierstrass este "depășit dincolo de recunoaștere" - în toate punctele!
În 1904, matematicianul suedez Helge von Koch, în articolul „Pe o curbă continuă, care nu are tangențială“ descrisă o altă curbă continuă, rupt la toate punctele, care se datorează simplității construcției a fost un exemplu remarcabil de un fractal. Cu curba Koch începem studiul fractalilor.
Fractalii în C ++ pentru Ch--
Curve Koch în toate detaliile frumuseții sale
Pentru a obține Curba lui Koch, segmentul de linie dreaptă este împărțit în trei părți egale, iar pe segmentul central construim un triunghi echilateral, după care se elimină baza triunghiului. Linia întreruptă rezultată din patru segmente reprezintă un șablon (șablon, generator), de-a lungul căruia este construită curba Koch.
Aplicând șablonul pe fiecare din cele patru segmente ale șablonului, obținem prima aproximație constând din 16 segmente. Apoi, aplicați un șablon pe fiecare segment al curbei rezultate, găsim cea de-a doua aproximare, formată din 64 de segmente. În limită, se obține curba Koch.
Pentru a construi Curve Koch și alte fractale, acest articol va utiliza un program standard care conține
Funcția de creație Trafresh Traf
Avem nevoie de o funcție care, din coordonatele capetelor segmentului AB, va calcula coordonatele tuturor punctelor nodale ale șablonului. Pentru a crea o astfel de funcție, vor fi necesare cunoștințe la nivelul clasei a IX-a a liceului. Formulele pentru coordonatele tuturor punctelor nodale ale șablonului Curve Koch sunt prezentate în figura din dreapta.

În stânga este funcția Traf. care are cinci argumente: coordonatele capetelor segmentului (xA, yA), (xB, yB) și parametrul k. Coordonatele punctelor nodurilor sunt stocate în celulele matricei: knx [] și kny [] (din cuvântul "nod" - "nod").
La construirea stencilului (aproximație zero), setăm k = 0, apoi coordonatele nodurilor intră în celulele inițiale ale matricelor. În aproximările rămase, o valoare diferită de zero a argumentului k este folosită pentru a evita suprapunerea coordonatelor.
Funcția fractală fractală
Această funcție construiește un fractal. În mod implicit, centrul sistemului de coordonate dreptunghiulare cartezian este situat în centrul ferestrei, iar axele pozitive au tăiat segmente individuale la limite. Dacă se dorește, operatorul gluOrtho () poate schimba sistemul de coordonate. Cum se face acest lucru este descris în detaliu în articolul "OpenGL în C ++ pentru Cp -".
Pentru a înțelege mai bine structura acestei funcții, o scriem separat pentru aproximările zero și primele. Pentru a calcula numai aproximația zeroth (programul din stânga jos), controlul este transferat la funcția Traf. iar linia orizontală centrală a ferestrei A (-1, 0), B (1, 0) se transformă într-un șablon. Deoarece k = 0, coordonatele nodurilor sunt în primele cinci celule ale matricelor knx [] și kny [].

Pentru a calcula doar prima aproximare (programul din partea dreaptă sus), adăugăm doi operatori ai buclului for. Primul își amintește coordonatele nodurilor de stencil obținute în etapa anterioară în tabelele kn1x [] și kn1y [] (declarate în interiorul funcției, deoarece nu sunt folosite nicăieri altundeva). Cel de-al doilea operator este împărțit cu un șablon în nodurile segmentului șablonului propriu-zis. Argumentul k este înmulțit cu 4 de fiecare dată, astfel încât în matricele knx [] și kny [], capetele tuturor r = 16 segmente ale primei aproximări se dovedesc a fi.
Toate aproximările ulterioare necesită de fiecare dată adăugarea a doi operatori identici, deci este recomandabil să creați un singur proces folosind un operator de buclă externă. Iată cum arată funcția în cazul general:

Numărul de segmente r în fiecare aproximație este egal cu 4 în gradul corespunzător.
Funcția Draw și principala funcție principală a programului
Aceste funcții sunt descrise în detaliu în articolul OpenGL în C ++ pentru Ch--.
Comenzile din afara zonei verzi a funcției Draw activează procesul de desenare. În interiorul zonei verzi, primii doi operatori fixează culoarea și grosimea liniilor. Parantezele operatorului glBegin () / glEnd () conțin coordonatele punctelor care sunt conectate în perechi în linii drepte folosind argumentul GL_LINES.
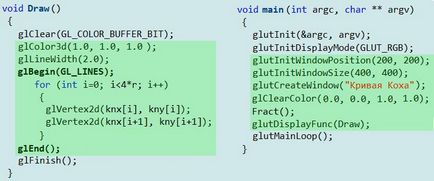
Toate comenzile sunt situate în afara zonei verzi a funcției principale. să construiască biblioteca OpenGL în C ++ și să o pună în acțiune. Operatorii din interiorul zonei verzi sunt fixați secvențial: locația ferestrei pe ecran, dimensiunile acesteia, dau numele ferestrei, deschideți-o și setați culoarea. Apoi sunt activate funcțiile Fract și Draw.
Iată cum arată:
Declamați parametrul de decalaj al celulei la. Numărul de segmente din aproximarea r și numărul de aproximări n.
Colectăm întregul program într-un singur întreg
Puteți obține cea de-a 5-a aproximare, dar nu va face modificări vizibile ale desenului.
Fractalii în C ++ pentru Ch--
Snowflake și Antisnazhinka Koch.
«Un brad dintr-un vas dulce de ceai»
Aplicați șablonul Koch Koch pe laturile triunghiului drept. Ca rezultat, obținem prima aproximare. Împărțim segmentul următoarei aproximări cu șablonul și în limita pe care o obținem în Snowflake of Koch.
Pentru Koch Snowflake, puteți folosi programul fractal. făcând mici schimbări în funcția de construire a unui fractal.
Funcția fractală fractală
Această funcție diferă de cea pentru Curve Koch de partea superioară (primele șase linii).
Definirea coordonatelor capetelor bazei inferioare a triunghiului A (-0.75, -0.5), B (0,75, -0.5) și găsiți al treilea nod C din condiția ca triunghiul din dreapta.
Aplicăm un șablon pe rând pe toate laturile triunghiului: de trei ori ne întoarcem la funcția Traf. dând valori la parametrul k = 0, 4, 8. Obținem o aproximare zero a 12 segmente cu coordonatele nodurilor din celulele dorite ale matricelor. Mai mult, construirea fractalului se face conform scenariului deja cunoscut.
Snowflake și Snowflake Koch
Dacă șablonul este proiectat astfel încât triunghiurile să fie direcționate spre interior, obținem Koch's Anti-Snowflake. Pentru a face acest lucru, schimbați semnele programului fractal în mijlocul semnelor operatorilor treia și a patra (care sunt evidențiate în roșu) de la plus la minus. Astfel arată Antisnazhinul lui Koch în a doua și a cincea aproximări:
A fost la Paști. În timp ce schimbau semnele de la plusuri la minus în operatori pentru a obține Koch's Anti-Snowball, difuzarea Descenderii Sfântului Foc din Ierusalim a început la televizor. Această vedere ma afectat atât de mult încât am reușit să schimb doar un semn. Pe ecran apare "trimis de sus" un fractal uimitor! O voi numi în onoarea noastră - "Ceainic dens Yolka"! Bucurați-vă!
Fractalii în C ++ pentru Ch--
"Funcția Matryoshka". Crearea copacilor
Când se construiesc fractali, se folosesc adesea "funcții matrioshka", care se transformă "în ei înșiși". În acest caz, nu este nevoie să creați un șablon, deoarece este deja încorporat în interiorul acestor funcții.
Iată o schemă simplă a funcției-matryoshka:

Această funcție este de la un argument: Matr (n). În interiorul bretelelor curbate ale operatorului ciclului, se întoarce spre ea însăși. reducerea argumentului cu 1. Fără declarația condiționată, programul se blochează.
Această funcție va fi de n ori "neautorizată" pentru a ieși din bucla, de fiecare dată când scade n cu unu. După ce parametrul n atinge zero, operatorul condițional elimină apelul funcției în sine și programul "în mod legitim" iese din bucla. Atunci nu va fi sanctionat n ori in ciclu, crescand de fiecare data cu n la 1. Daca la intrare reiese ca i = 0. atunci din acest punct ciclul va continua sa functioneze. Acest lucru se va întâmpla până când nu ajunge la valoarea inițială. "Funcția Matryoshka" generează un proces "ramificat", utilizat în construcția de fracturi.
Pentru a crea un arbore fractal, luați în considerare o ramificație AB a lungimii L cu o pantă a pe axa orizontală. Dacă sunt cunoscute coordonatele punctului inițial A, atunci coordonatele punctului final B pot fi calculate de către elevul din clasa 7B a școlii secundare. Formulele de mai sus pentru xB și yB vor fi folosite pentru a construi fractalul în funcția Fract.
Curbe Levy și Pitagora Copacii sunt strâns legate de fractali, care sunt numite Dragonii din cauza asemănării lor la imagini de dragoni din China.
Modurile de creare a curbelor Levi și Pythagoras sunt similare. Ele diferă doar prin șabloane, care sunt atașate din exterior la cele două picioare ale unui triunghi dreptunghiular.
Dacă aceste șabloane sunt trimise alternativ în direcții diferite față de picioare, atunci Dragonii se vor întoarce.
Dragonii din insula Levi
Începem să construim curba Levy. dar șablonul este atașat la picioarele triunghiurilor în unghi drept, direcționându-l alternativ în direcții diferite. Pentru a face acest lucru, program de prelevări în funcția de a doua declarație atunci când fracționare se referă la sine schimba punctele B și C (programul în care sunt marcate în roșu). Operatorul ar trebui să arate astfel: Fract (x B. B. B. C. C. y C. n-1). Balaurul apare pe ecran.

Dragonii arata frumos pe ecran, trebuie sa corectati culoarea liniei si sa inlocuiti parantezele operatorului in program (acestea sunt indicate in desene).
Același lucru se poate face și cu Insulele Levi și obțineți "insula" Dragonii:

Construim copacul lui Pitagora. dar ecran direct laturile opuse ale picioarelor de ventilator triunghi, și apare pe ecran Dragon Pitagora. Pentru a face acest lucru, programul pifagor în funcția de a construi fractale în prima fracționare declarație se referă la funcția Traf sub semnul swap ciclu argumentele matrice (marcate cu roșu). Operatorul trebuie să arate ca: Traf (KNX [i + 1], Kny [i + 1], KNX [i], Kny [i], 5 * r).
În stânga în figură este Dragonul lui Pythagoras în a 4-a aproximare cu un "ventilator" colorat de triunghiuri. Adevărat, este mai mult ca un bombardier cu rază lungă de acțiune Tu-22M3 care zboară pe o misiune de luptă. Și în figura corectă - Dragonul pictat al lui Pythagoras în armonizarea a zecea.
Fractalii în C ++ pentru Ch--
Dă-mi o femeie albă și albă.
O voi schimba într-o albastră
Rămâne să-și îndeplinească promisiunea și să-i ajute pe poet să-i remakeze albastru, alb cu albastru. Această femeie din imagine Henri Matisse este numită "Naked with orange". După mastering OpenGL și C ++, putem desena cu ușurință Snowflake și Snowflake Koch. "Un brad al unui ceainic dens", Krivoy Levy. "Blow the wind" al lui Pythagoras și transforma-l într-un dragon.

Cu toate acestea, atunci când încercați să remake o alb, alb albastru, se prăbușește și veți obține "Dragon copt cu portocale." Întrebarea este, de ce? Și de ce nu? Acest lucru este de asemenea bun! Rămâne doar să fugi pentru sticla "Putinki"!
Totul sa întâmplat accidental, așa cum era planificat.