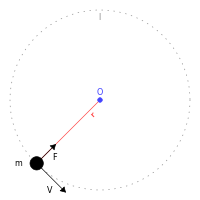
Forța centripetală F transformă un corp de masă m care se deplasează cu viteza V în jurul punctului O de-a lungul unei traiectorii circulare cu raza r
Forța centripetală este numele acelei componente a forțelor care acționează asupra corpului. care face ca corpul să se rotească (adică să se miște de-a lungul unei traiectorii a cărei rază de curbură în punctul în care se află corpul nu poate fi considerată infinită). Aceasta este o componentă direcționată perpendicular pe vectorul de viteză instantanee a corpului.
Pentru a forma o traiectorie cu o rază de curbură la un anumit punct r. forța centripetală F c = m a c = m v 2 r = m ω 2 r = ma_ = m >> = m \ omega ^ r>. unde c> este accelerația centripetală la un anumit punct, m este masa corpului, v este viteza sa la un anumit punct și ω este viteza unghiulară la un anumit punct.
Dacă acordăm atenție rotației traiectoriei corpului, putem să individualizăm accelerația a c → >>>. perpendicular pe viteza. Această accelerație schimbă direcția mișcării corpului, întoarce traiectoria și formează o curbură a razei r la viteză v această accelerație ar trebui să fie egală cu v 2 r >>>. sau, ceea ce este același, ω 2 r r>. unde ω este viteza unghiulară a corpului într-un anumit punct față de centrul de rotație instantanee (relația dintre prima formulă și cea de-a doua este evidentă, ținând seama de faptul că v = ω r). Această componentă a accelerației se numește accelerație centripetală. Conform celei de-a doua legi a lui Newton. accelerația observată a corpului corespunde cu suma forțelor care acționează asupra ei. Acest lucru este adevărat în cadrele inerțiale de referință. și conform principiului lui D'Alembert, acest lucru, odată cu introducerea forțelor de inerție corespunzătoare. adevărat și în cele non-inerțiale. Componenta forțelor care acționează asupra corpului, care corespunde accelerației centripetale, se numește forța centripetală (F c → = m a c → >> = m >>>).
Forța centripetală nu este o forță independentă și este doar rezultatul unei extinderi formale a sumei tuturor forțelor care acționează asupra corpului în două componente - de-a lungul și de-a lungul tangentei la traiectoria mișcării. În cazul unui echilibru (adică, cu o viteză unghiulară constantă) deplasarea corpului de-a lungul unui traseu circular din cauza singura forță care acționează în direcția centrului de rotație (de exemplu, forțează tensiunea fire, care face legătura între corpul spre centru, sau în cazul conducerii pe o orbită circulară într-un câmp de gravitație) toata aceasta forta este centripetala. Ea este direcționată perpendicular pe vectorul de viteză, nu completează lucrarea pentru cercul complet, energia cinetică a corpului nu se schimbă. Această mișcare poate continua pe termen nelimitat.
În general, atunci când călătoriți pe orice traiectorie diferită de cea circulară, centrul de rotație nu se află în direcția sumelor forțelor care acționează asupra corpului. De exemplu, atunci când Pământul se mișcă în jurul Soarelui pe orbita sa eliptică, Pământul acționează asupra forței de atracție reciprocă a Pământului și Soarelui devine centripet pe deplin numai în afeliu și periheliu. În acest caz, componenta tangențială a forței reacției de comunicare efectuează o activitate care duce la o creștere a energiei cinetice a corpului (în timpul accelerației) sau la o scădere a acestuia (în timpul frânării). Acest lucru are loc periodic în univers atunci când corpurile celeste se deplasează de-a lungul orbitelor eliptice Keplerian în jurul centrului de greutate comun, deoarece lucrarea forțelor de comunicare pentru o revoluție completă este zero. De asemenea, datorită avansării sistematice a centrului de rotație instantanee prin deplasarea punctului de aplicare a forței, se desface o sforă, de exemplu.
Dar și viteza, accelerația și traiectoria corpurilor depind de sistemul de referință ales, alegerea sistemului de referință depinde de ce parte a cantității de forță necesară pentru a lua în considerare centripet. În special, se deplasează în sistemul de referință conectat direct la corpul în mișcare, vom reduce în mod natural calea spre un punct fix în centrul cadrului de referință, și, prin urmare, nu poate, în contextul sistemului de vorbire de referință despre accelerația centripetă a corpului, sau a puterii corespunzătoare . Pe de altă parte, merge la sistemul de referință prin rotație în ceea ce privește organismele, am să-l traiectoria curbată a organelor corespunzătoare accelerației centripete și, în consecință, forța centripetă.
Cu conceptul de "forță centripetală" și tranziția de la cadrul de referință inerțial la sistemul rotativ neinerțial, conceptul de "forță centrifugă" este strâns legat.
Datorită complexității înțelegerii trecerile de la un cadru la altul, mai ales dacă acestea sunt în mișcare una față de cealaltă, cu o accelerare modifică în mod dinamic, conceptul de forțe centripete și centrifuge provoacă multe controverse și neînțelegeri.
- Frish SA și Timoreva Curs de fizică generală, Manual pentru fizică și matematică și Facultăți fizico-tehnice ale universităților de stat, vol. I. M. GITTL, 1957