De ceva timp m-am interesat de astfel de figuri, care la prima vedere par obișnuite și, uitându-te îndeaproape, poți vedea că ceva e în neregulă. Principalul interes pentru mine a fost așa-numitele cifre imposibile, privirea la care dă impresia că nu pot exista în lumea reală. Voiam să știu mai multe despre ele.
"Lumea Imposibilităților" este unul dintre subiectele cele mai interesante, care a cunoscut o dezvoltare rapidă la începutul secolului al XX-lea. Cu toate acestea, mult mai devreme, mulți oameni de știință și filosofi au abordat această problemă. Chiar și formele simple tridimensionale, cum ar fi un cub, o piramidă, un paralelipiped, pot fi reprezentate ca o combinație a mai multor figuri situate la distanțe diferite de ochiul observatorului. Întotdeauna în același timp trebuie să existe o linie de-a lungul căreia imaginea pieselor individuale să fie combinată într-o imagine completă.
"Figura imposibilă este un obiect tridimensional executat pe hârtie, care nu poate exista în realitate, dar care totuși poate fi văzut ca o imagine bidimensională". Acesta este unul dintre tipurile de iluzii optice. o figură care la prima vedere pare a fi o proiecție a obiectului obișnuit tridimensional, la o examinare mai atentă a cărei legături contradictorii ale elementelor figurii devin vizibile. Se creează o iluzie că o astfel de figură nu poate exista în spațiul tridimensional.
În fața mea a apărut întrebarea: "Există cifre imposibile în lumea reală?"
1. Exprimați cum sunt create formele ireale.
2. Găsiți zonele de aplicare a unor forme posibile.
1. Să studieze literatura de specialitate pe tema "Cifre imposibile".
2.Compoziția de clasificare a cifrelor posibile.
3. Luați în considerare modalitățile de a construi cifre imposibile.
4.Creați o cifră imposibilă.
Tema lucrării mele este relevantă deoarece paradoxurile de înțelegere reprezintă unul dintre semnele unui tip de potențial creativ pe care îl posedă cei mai buni matematicieni, oameni de știință și artiști. Multe lucrări cu obiecte ireale pot fi atribuite "jocurilor matematice intelectuale". Pentru a simula o lume similară este posibilă numai cu ajutorul formulelor matematice, oamenii nu-și pot imagina. Și pentru dezvoltarea imaginației spațiale, cifrele imposibile se dovedesc a fi utile. O persoană neobișnuit creează în jurul său ceea ce va fi simplu și ușor de înțeles pentru el. Nici nu-și poate imagina că unele obiecte din jurul lui pot fi "imposibile". De fapt, lumea este una, dar poate fi văzută din diferite unghiuri.
Cifrele imposibile sunt destul de comune în gravuri vechi, picturi și icoane - în unele cazuri, suntem cu perspective clare de erori de transmisie, în altele - cu distorsiunea deliberată datorită concepției artistice.
În pictură japoneză și persană medievală obiecte imposibile sunt o parte integrantă a stilului de arta de Est, oferind doar o schiță generală a imaginii, detaliile care „trebuie să“ gândească în audiență pe cont propriu, în funcție de preferințele lor. Aici este școala din fața noastră. Atenția noastră este atrasă de structura arhitecturală în fundal, care neconcordanța geometrică este evidentă. Acesta poate fi interpretat ca peretele interior al camerei, și ca peretele exterior al clădirii, dar ambele interpretări sunt greșite, pentru că avem de-a face cu un plan, este în același timp un exterior și un perete exterior, care este, pictura descrie un obiect tipic imposibil.

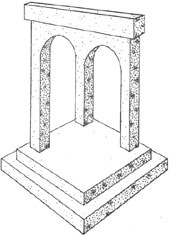
Imaginile cu o perspectivă distorsionată sunt deja la începutul primului mileniu. În miniatură din cartea lui Henric al II-lea, creată înainte de 1025 și păstrată în biblioteca de stat bavareză din Munchen, a pictat Madonna și Child. Pictura descrie o boltă compusă din trei coloane, coloana de mijloc conform legilor perspectivei ar trebui să fie situată în fața Madonei, dar este în spatele ei, ceea ce oferă imaginii un efect de nerealitate.

"Cifrele imposibile" sunt împărțite în 4 grupe. Deci, mai întâi:
Triunghi uimitor - tribar.
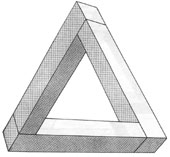
Iată câteva exemple de cifre imposibile bazate pe tribar.

Tribar triform deformat
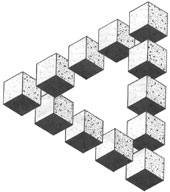
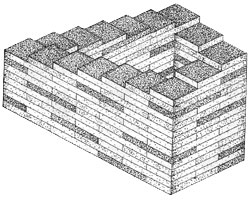
Această cifră este adesea numită "Scara fără sfârșit", "Scara veșnică" sau "Scara Penrose" - prin numele creatorului său. Se mai numește și "cale ascendentă și descendentă continuu".
"Scara fără sfârșit" a fost folosită cu succes de artistul Maurits K. Escher, de această dată în litografia sa "Ascent and Descent", creată în 1960.
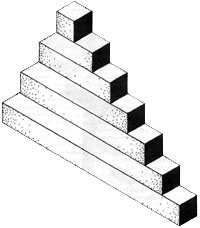
Creatorii acestei scări au folosit linii paralele în dezvoltarea părților finale ale blocurilor situate la aceeași distanță; se pare că unele blocuri sunt răsucite pentru a se potrivi cu iluzia.
Următorul grup de figuri sub denumirea generală "Furcă spațială". Cu această figură, intrăm în esența și esența imposibilului. Poate că aceasta este cea mai numeroasă clasă de obiecte imposibile.
Din punct de vedere practic, acest trident ciudat sau un mecanism sub forma unei bretele este absolut inaplicabil. Unii oameni o numesc pur și simplu "o greșeală enervantă". Un reprezentant al industriei aerospațiale a sugerat utilizarea proprietăților sale în construcția unei furci interdimensionale de reglare a spațiului.
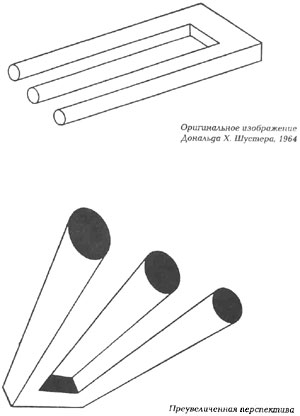
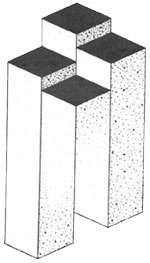
Turnul cu patru coloane gemene.
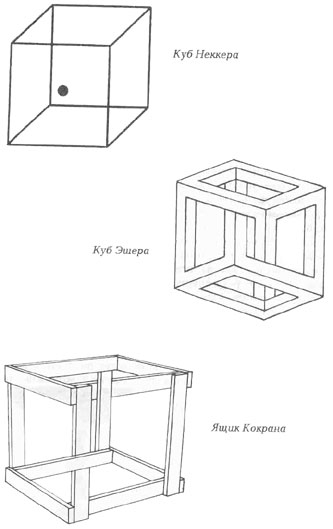
Nu este un obiect imposibil, dar este o figură în care parametrul de adâncime poate fi perceput ambiguu.
Când privim în cubul Necker, observăm că fața cu punctul se află undeva în față, apoi în fundal, sare dintr-o poziție în alta.
„Tatăl“ figuri imposibile este considerat un artist suedez Oscar Reutersvärd. artistul suedez Oscar Reutersvärd, pentru a crea imagini de experți figuri imposibile susțin că prost versat în matematică, dar, cu toate acestea, a ridicat arta sa la rangul de știință, creând o întreagă teorie a creării de cifre imposibile de un anumit număr de șabloane.
El a împărțit cifrele în două grupuri principale. Unul dintre ei a numit "cifre adevărate imposibil". Acestea sunt imagini bidimensionale ale corpurilor tridimensionale, care pot fi pictate pe hârtie și le pun umbre, dar nu au o adâncime monolitică și stabilă.
Un alt fel este cifrele dubioase imposibil. Aceste cifre nu reprezintă corpuri întregi întregi. Ele sunt unirea a două sau mai multe figuri. Ele nu pot fi colorate și nici nu le pot pune lumină și umbre.
Cifra adevărată imposibilă constă dintr-un număr fix de elemente posibile, iar un dubios "pierde" un anumit număr de elemente, dacă este urmat cu ochii.
O versiune a acestor cifre imposibile este foarte ușor de realizat, iar mulți dintre cei care trag mecanic geometric
În figură, vedem trei variante de cifre discutabile imposibile. La stânga este un baril de trei șapte, construit din șapte linii, în care trei grinzi se transformă în șapte. Figura în mijloc, construită din trei linii, în care un fascicul se transformă în două bare rotunde. Cifra din dreapta, construită din patru linii, în care două bare rotunde se transformă în două grinzi
Cifre imposibile sunt posibile!
Mulți cred că cifrele imposibile sunt cu adevărat imposibile și nu pot fi create în lumea reală. Dar trebuie să ne amintim că orice desen pe o foaie de hârtie este o proiecție a unei figuri tridimensionale. Prin urmare, orice figură trasată pe o foaie de hârtie trebuie să existe în spațiul tridimensional. Obiectele imposibile din imagini sunt proiecțiile obiectelor tridimensionale, ceea ce înseamnă că obiectele pot fi realizate sub formă de compoziții sculpturale. Există multe modalități de a le crea. Una dintre ele este utilizarea de linii curbe ca laturile unui triunghi imposibil. Sculptura creată pare imposibilă doar dintr-un singur punct. Din acest punct, curbele laturilor arata drept, iar obiectivul stabilit va fi atins - se creeaza un obiect real "imposibil".
Artistul rus Anatoli Konenko, contemporanul nostru, a împărțit cifrele imposibile în două clase: unele pot fi modelate în realitate, în timp ce altele nu pot. Modele de cifre imposibile sunt numite modele Ames.
Am făcut modelul lui Ames cu cutia mea imposibilă. Am luat patruzeci și doi de cuburi și le-am lipit împreună, a ieșit un cub, în care lipsește o parte a coastei. Am observat că pentru a crea o iluzie completă, aveți nevoie de unghiul drept și iluminarea corectă.
Am studiat cifrele imposibile folosind teorema lui Euler și am ajuns la următoarea concluzie: Teorema lui Euler, adevărată pentru orice polyhedron convex, este incorectă pentru figuri imposibile, dar adevărată pentru modelele lor Ames.
Creez cifrele mele imposibile, folosind sfatul lui O. Rutersvard. Am desenat șapte linii paralele pe hârtie. Le-am legat de jos, cu o linie întreruptă, și deasupra le-am dat formă de paralelipipede. Priviți-o mai întâi de sus și apoi de jos. Există infinit multe astfel de cifre. Vedeți atașamentul.
Câteva cifre imposibile găsesc o aplicație neașteptată. Oscar Rutersward spune în cartea "Omojli ga figurer" despre utilizarea desenelor de imp-art pentru psihoterapie. El scrie că imaginile cu paradoxurile lor provoacă surpriză, accentuează atenția și dorința de a descifra. Psihologul Roger Shepard a folosit ideea unui trident pentru imaginea lui despre un elefant imposibil.
În Suedia, ele sunt folosite în practica dentară: atunci când examinăm imaginile în sala de așteptare, pacienții sunt distrași de gândurile neplăcute în fața cabinetului dentistului.
Cifre imposibile au inspirat artiștii pentru a crea o tendință cu totul nouă în pictura, numită imposibilizmom. Pentru imposibilisti sunt artistul olandez Escher. Stiloul său aparține faimoaselor litografii "Vodopad", "Ascent and descence" și "Belvedere". Artistul a folosit efectul "scară fără sfârșit", descoperit de Rutesaward.
În străinătate, pe străzile orașelor, putem vedea incarnările arhitecturale ale unor figuri imposibile.
Cea mai faimoasă utilizare a cifrelor imposibile în cultura populară este logo-ul concernului auto Renault
Matematicienii susțin că pot exista palate în care puteți merge în jos pe scări. Pentru a face acest lucru, trebuie doar să construiți o astfel de structură nu în spațiul tridimensional, ci, dimpotrivă, în patru dimensiuni. Și în lumea virtuală, care ne este deschisă prin tehnologia modernă a calculatoarelor, și nu este posibil acest lucru. Așa se fac astăzi ideile unui om care, la începutul secolului, crede în existența unor lumi imposibile.
Cifrele imposibile fac ca mintea noastră să vadă mai întâi ce nu ar trebui să fie, apoi căutați răspunsul - ceea ce se face este greșit, ceea ce este ascuns în punctul culminant al paradoxului. Iar răspunsul uneori nu este atât de ușor - este ascuns în percepția optică, psihologică, logică a desenelor.
Dezvoltarea științei, nevoia de a gândi într-un mod nou, căutarea frumuseții - toate aceste cerințe ale vieții moderne ne obligă să căutăm noi metode care pot schimba gândirea spațială și imaginația.
După ce am studiat literatura de specialitate pe această temă, am reușit să răspund la întrebarea "Există cifre imposibile în lumea reală?" Mi-am dat seama că se pot face cifre imposibil și nerealiste de la sine. Am creat modelul Ames al "Cubei Imposibile" și am testat teorema lui Euler asupra lui. După ce am examinat căile de a construi figuri imposibile, am putut să-mi desenez figurile imposibile. Am reușit să arăt asta
Concluzia 1: Toate figurile imposibile pot exista în lumea reală.
Concluzia2: Teorema lui Euler, adevărată pentru orice polyhedron convex, este incorectă pentru figuri imposibile, dar este adevărată pentru modelele lor Ames.
Concluzia3: Există încă multe zone în care cifrele imposibile vor fi utilizate.
Astfel, putem spune că lumea figurilor imposibile este extrem de interesantă și diversă. Studiul unor cifre imposibile este destul de important din punct de vedere al geometriei. Lucrarea poate fi folosită în clasele de matematică pentru a dezvolta gândirea spațială a studenților. Pentru oamenii creativi înclinați spre invenție, figurile imposibile sunt un fel de pârghie pentru a crea ceva nou, neobișnuit.
Leptin Karl Rapsodie geometrică. - M. Knowledge, 1984, -176 pag.
Penrose L. Penrose R. Obiecte imposibile, Quantum, No. 5,1971, p.26