De mult timp am urmărit ideea de a trece prin algoritmii-cheie de exploatare a datelor. să sistematizăm cunoștințele existente și să facem o analiză cu exemple. De fapt, acest articol și comemorarea începutul acestei serii. De exemplu, se va folosi mediul software R. Am scris despre asta într-unul din ultimele postări.
Regresie liniară
Strict vorbind, regresia liniară nu este un algoritm de extragere a datelor. Aceasta este una dintre metodele care au venit din statistici. În statistici, sub regresie, este de obicei menită să prezică, într-o formă sau alta. Există multe tipuri diferite de regresii, însă în centrul oricare dintre ele există aceeași idee: să construim un model care să lege valoarea estimată cu datele originale (predictorii), minimizând eroarea.
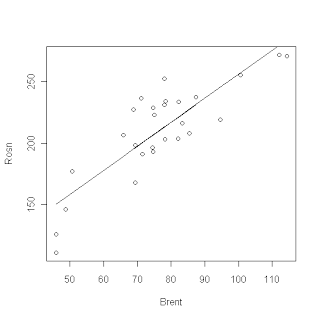
Regresia liniară este cea mai simplă formă de regresie. Luați în considerare, de exemplu, o regresie liniară cu o valoare predictivă și una predicată. O astfel de regresie este ușor de atras pe harta X-Y. Pentru aceasta, marchează valorile predictorului de-a lungul axei X și valorile valorii predictive de-a lungul axei y. Apoi, o regresie liniară simplă este o linie dreaptă, realizată astfel încât să minimizeze discrepanța dintre valorile reale ale valorii estimate și punctele de pe linia corespunzătoare valorilor predictorului.
În limba matematică, putem descrie modelul nostru linear sub forma unei ecuații: Y = a + b * X, unde X este un predictor sau date brute și Y este valoarea prezisă. Și sarcina însăși este reformulată sub forma: găsiți coeficienții a și b care minimizează magnitudinea erorii.
Când modelul este construit și se găsesc coeficienții, putem folosi ecuația rezultată pentru a prezice valorile necunoscute.
Să luăm un exemplu din domeniul finanțelor. Nu este un secret pentru nimeni că prețurile acțiunilor companiilor petroliere sunt în mare măsură dependente de prețurile petrolului. În aproximarea zeroth, putem presupune asta
Prețul unui baril de petrol + O anumită constantă
Dacă putem determina constanta și coeficientul, atunci putem prezice prețul stocului pentru prețul petrolului. Dacă există o abatere, puteți să cumpărați o răspândire și să câștigați, în mod teoretic, natural.
Și acum practică, să luăm R și să efectuăm o regresie liniară a prețurilor acțiunilor Rosneft la prețul petrolului. Datele inițiale pot fi găsite aici:
rezultat:
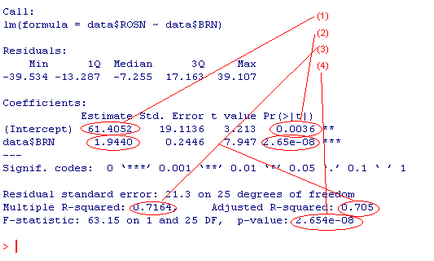
În figură, coeficienții de interes pentru noi sunt notați cu (1). Prin substituirea lor în ecuația de regresie, obținem expresia: ROSN = 61.405 + 1.944 * Brent plus față de valorile coeficientilor de fapt, R ne arată cantitatea de erori sau deviația standard pentru fiecare coeficient. Dar asta nu e tot. De exemplu, ar putea fi interesant pentru noi dacă cel puțin unii dintre coeficienții noștri explică deloc. Pentru a testa acest lucru, am prezentat ipoteza nulă că, de exemplu, coeficientul de 61405 este doar rezultatul erorii și valoarea sa poate fi neglijată. Pentru a testa această ipoteză, se folosește testul t Student. Aici, R pentru noi a face toate lucrările, calcularea valorii în sine ca t și gradul de semnificație a ipotezei noastre Pr (> | t |). Deci, în cazul nostru, valoarea (două) 0,0036 înseamnă că suntem pe 100 * (1-.0036) = 99,64% consideră că termenul constant în această expresie este non-zero. Apoi, putem verifica cât de precis modelul nostru descrie datele. Pentru aceasta se folosesc coeficienții R 2 (3). Cu cât valoarea acestor valori este mai apropiată de 1, cu atât mai bine. 1 este rezultatul ideal, ceea ce înseamnă că modelul descrie datele 100%. Și, în sfârșit, ultimul lucru pe care îl putem verifica este măsura în care valoarea estimată depinde de predictori. Pentru aceasta, ipoteza nulă este avansată, că valoarea prezisă nu depinde deloc de predictori. Pentru această ipoteză, se determină valoarea p (4). În cazul nostru, sa dovedit a fi 2,65 * 10 ^ -8. Ie putem avea încredere la 99,99999735% că valoarea estimată depinde într-adevăr de predictori. De obicei, este mai bine să ne uităm mai întâi la acest parametru, deoarece determină cât de adecvat este modelul nostru. Da, apropo, graficul este ușor mai mare, arată doar datele noastre și rezultatul regresiei liniare.
Ce se întâmplă dacă datele mele nu sunt descrise de o linie dreaptă?
regresie liniară cu un predictor este cea mai simplă versiune a regresiei, în practică, un număr de posibile complicații care pot rezolva probleme mult mai complexe: 1) adăugarea mai multor predictori - predictori suplimentari pot adăuga mai multe informații pentru a modela și de a îmbunătăți, astfel, rezultatele. Ecuația regresiei liniare poate avea atunci următoarea formă: Y = a + b1 * X1 + ... bn * Xn 2) un preliminar predictori de transformare - Construirea de predictori în grad sau rădăcini de extracție este o modalitate de a crește posibilitatea de regresie liniară. În practică, este adesea necesar să se efectueze un număr mare de transformări diferite pentru a afla care dintre ele va oferi cea mai bună estimare. 3) în ecuația modelului poate fi adăugat la produs care conține predictori membre 4) apare adesea problema de a prezice probabilitatea unui eveniment. Ie valoarea prezisă presupune numai două valori de 1 și 0 sau da și nu. Regresia logistică este utilizată pentru a rezolva astfel de probleme. Din fericire, toate aceste și multe alte adăugări sunt implementate în R și sunt gata de utilizare. Informații despre modul de utilizare a acestora pot fi obținute prin tastarea în interfața de comandă R.
SergE San Francisco, California, Statele Unite ale Americii Hi, Sunt inginer de software de top într-o companie de web mare. Interesați în principal de extracția de date și învățarea în mașină. Limba mea de programare "nativă" este Java, deși cred că Haskell și FP în general sunt mai bune. Am o experiență decentă cu stivele C # și .Net, de asemenea. În timpul liber, sunt fericit să concurez cu oamenii inteligenți pe Topcoder și Kaggle. Profilul meu TC este aici. Profilul Kaggle aici Dacă vrei să vorbești, trebuie doar să trimiți un mesaj: e d u n o v g o m a l l. c o m Vizualizați profilul meu complet