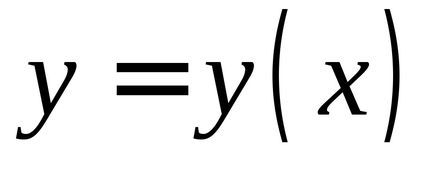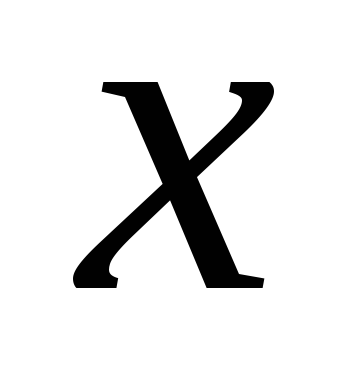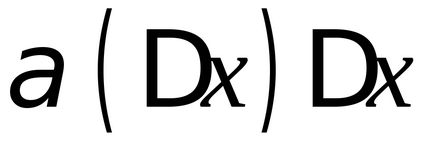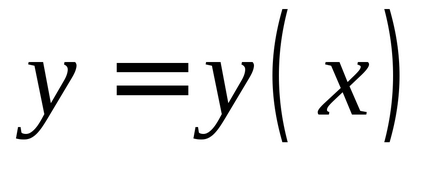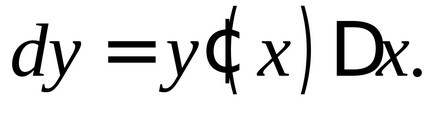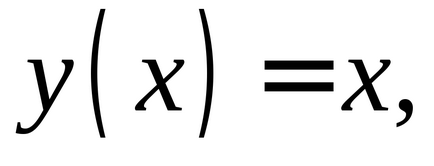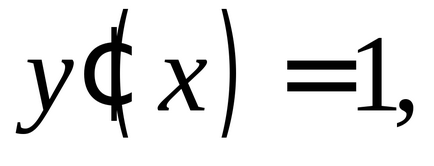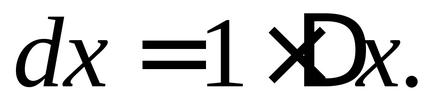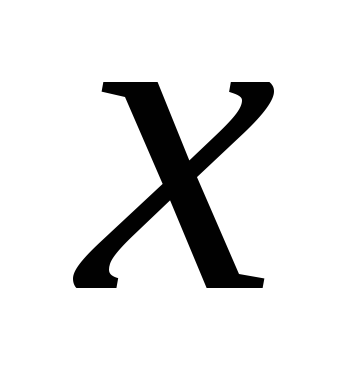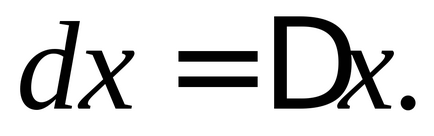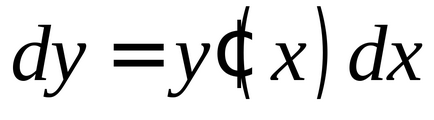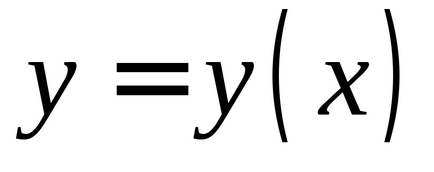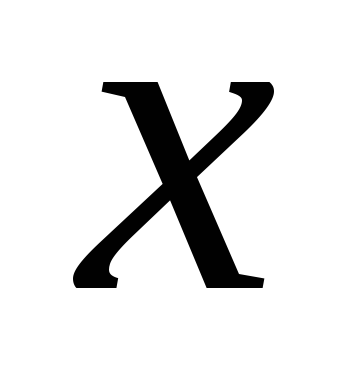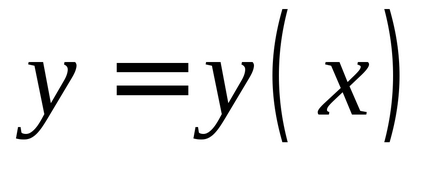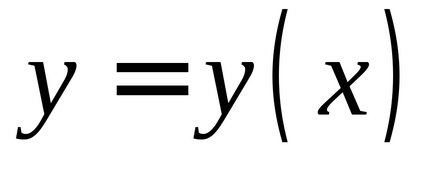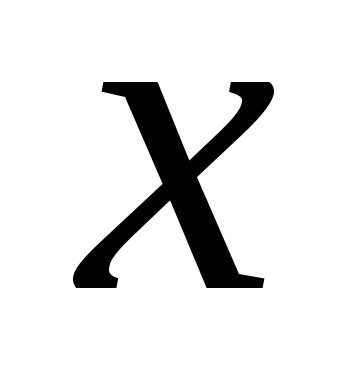În cazul în care
este diferențiată în acest punct, atunci creșterea în acest punct constă în două părți:- liniar cu privire lași- neliniar cu privire la, BM ordinea superioară a micșorării.Determinare. Funcție diferențială
în acest punctPartea principală a creșterii sale la acest punct se numește:
În cazul în care
prin urmareEste general acceptat că dacăEste o variabilă independentăAstfel, prin definiție.
THEOREM (privind legătura dintre continuitate și diferențiabilitate). Lăsați funcția
este diferențiată în acest punct, atunci este continuă în acest moment.
Dovada. Prin definiția diferențierii, creșterea funcției
este reprezentat în formă. Apoi, prin definiție, 2 înseamnă continuitateîn acest punct.
NOTĂ. Conversia nu este adevărată, adică nu orice funcție continuă este diferențiată (graficul unei funcții continue poate să nu aibă o tangență în toate punctele).
Articole similare