1. Care este cauza erorii nerecuperabile?
a) Faptul că modelul matematic al obiectului în studiu nu consideră că oricare și toate evenimentele care afectează starea obiectului, și faptul că membrii parametrilor de sarcini sunt specificate (număr sau funcție) se măsoară cu o eroare.
b) Faptul că operațiile aritmetice pe numere sunt efectuate atunci când există un număr limitat de biți din calculul pozițional folosit pentru scriere.
c) Faptul că aplicarea metodei numerice pot fi obținute nu exactă și valori aproximative ale funcției necunoscute, chiar dacă au făcut exact toată metoda prescrisă de calcul.
2. Unele valori ale t = 0,34 și k = 0,42 au fost măsurate cu până la 0,01. Găsiți erorile absolute și relative în determinarea valorii d = t · k = 0.1428.
a) Eroare absolută = 0,0075. eroare relativă = 0,053.
b) eroare absolută = 0,0077. eroare relativă = 0,051.
c) eroare absolută = 0,0077. eroare relativă = 0,054.
3. Fie p * valoarea exactă, a-aproximată a unui număr. Dați definiția erorii relative.
a) Eroarea relativă a aproximării a este cantitatea δa astfel încât
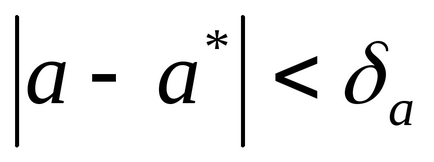
b) Eroarea relativă a aproximării a este o cantitate δa astfel încât, (a ≠ 0).
c) Eroarea relativă în aproximarea lui a este cantitatea
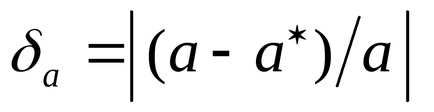
4. Determinați eroarea relativă a numărului aproximativ b = 2,3254 din eroarea sa absolută Δb = 0,01, rotunjind numărul pentru a corecta semnele.
a) Eroare relativă = 0,0078. b) eroare relativă = 0,0043.
c) eroare relativă = 0,0143.
5. Se măsoară volumul V = 2.385 m3 și densitatea ρ = 1400 kg / m3 a probei cu o precizie de 1 dm3 și respectiv 1 kg / m3. Găsiți erorile absolute și relative în determinarea masei probei m = V ∙ ρ = 3339 kg.
a) Eroare absolută = 3.895, eroare relativă = 0.0012.
b) eroare absolută = 3,786, eroare relativă = 0,0011.
c) eroare absolută = 3.657, eroare relativă = 0.0010.
7. Care este cauza apariției unei erori de rotunjire în soluția numerică a sarcinii?
a) Faptul că modelul matematic al obiectului studiat nu poate lua în considerare toate fenomenele care afectează starea obiectului fără excepție.
b) Faptul că operațiile aritmetice pe numere sunt efectuate atunci când există un număr limitat de biți din calculul pozițional folosit pentru scriere.
c) Faptul că aplicarea metodei numerice pot fi obținute nu exactă și valori aproximative ale funcției necunoscute, chiar dacă au făcut exact toată metoda prescrisă de calcul.
8. Definiți funcția spline.
a) Un polinom luând f (xi) la punctele xi se numește o funcție spline corespunzătoare unei funcții date f (x) și nodurilor xi (i = 0, 1, ..., n).
a) spline-funcția corespunzătoare acestei funcții, f (x) și xi noduri (i = 0, 1, ..., n), numit un polinom de forma în care, h - diferența grilă pas Δ Kyi - diferență finită de ordinul k.