z este un vector de zerouri, p este un vector de poli și k este un câștig.
Pentru trecerea de la reprezentarea polului-zero a unui sistem continuu la o funcție de transfer, transformarea
Efectuează descompunerea în fracțiuni simple a funcției de transfer, reprezentată ca un raport de două polinoame. Aici reziduurile sunt stocate în vectorul r. Polii sunt în vectorul p. câștigul este în k. Format [B, A] = reziduu (z, p, k), cu trei argumente de intrare și două sisteme de ieșire convertește o funcție de transfer pol-zero în reprezentarea.
Construcția răspunsului tranzitoriu (treapta de răspuns) a sistemului poate fi efectuată prin introducerea
în mod asemănător, sistemul de răspuns la impuls (impuls)
Pentru a determina răspunsul (ieșirea) sistemului la un semnal de intrare arbitrar, utilizați comanda lsim (...).
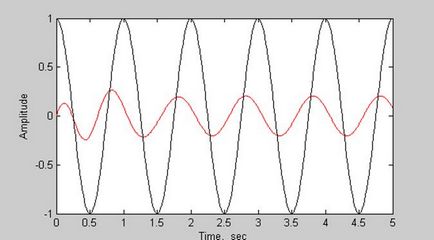
Un exemplu. Să determinăm semnalul de ieșire al unui sistem cu o funcție de transfer
și semnalul de intrare.
>> n = [20]; % Numitorul și numitorul funcției de transfer
>> t = linspace (0,5301); % Setarea intervalului de timp
>> u = cos (2 * pi * t); % Semnal de intrare
>> [y, x] = lsim (n, d, u, t); % Semnal de ieșire
>> xlabel ('Timp, sec');
Grafice ale semnalelor de intrare și ieșire
Caracteristicile de frecvență și grafice lor
Funcții MATLAB pentru calcularea și plotarea curbelor de răspuns în frecvență:
fft (x) - calculează transformarea discretă Fourier a vectorului x folosind algoritmi de transformare rapidă Fourier (FFT).
ifft (x) - calculează transformarea Fourier discretă inversă a vectorului x folosind FFT
fftshift - schimbă conversia fft din intervalul (0, 2π) la intervalul (-π, π)
frecvențele (n, d) - calculează răspunsul de frecvență al unui sistem continuu cu o funcție de transfer n (s) / d (s)
freqz (n, d) - calculează răspunsul de frecvență al unui sistem (discret) cu funcția de transfer n (z) / d (z)
bode (n, d) - Construiește o diagramă Bode a unui sistem continuu cu funcția de sistem n (s) / d (s).
desface (P) - corectează unghiurile de fază ale elementelor matricei unidimensionale P în tranziție
prin valoarea lui π.
Un exemplu de construire a unui răspuns de frecvență al unui sistem cu o funcție de transfer
set (gca, 'FontName', 'Times New Roman Cyr', 'FontSize', 8)
titlu ("Caracteristică de amplitudine - frecvență")
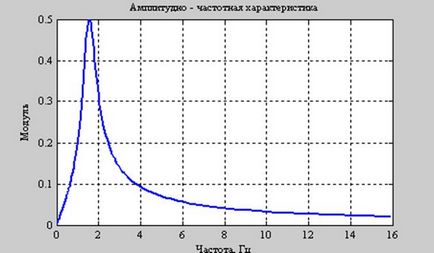
Un exemplu de construcție a unei diagrame Bode și a unui răspuns impuls
»% Desenarea unei diagrame de poli și zerouri
Funcția fft () în problemele de procesare a semnalelor este folosită, probabil, mai des decât toate celelalte. Acesta calculează transformarea discretă Fourier (DFT) a vectorului x prin expresie
lungimea vectorului x.
Aceeași funcție cu formatul
calculează o transformare Fourier discretă în n-punct. Dacă, atunci elementele lipsă ale matricei x sunt completate cu zerouri (zeropad). Dacă, atunci elementele suplimentare sunt aruncate.
Funcția x = ifft (X) calculează DFT inversă a secvenței X. Funcția x = ifft (X, n) calculează DFT invers D n.
Pentru calcularea funcțiilor fft () și ifft () se folosesc algoritmi de transformare Fourier rapidă (FFT). Acest algoritm are viteza maximă atunci când lungimea secvenței x este egală cu puterea lui 2. Prin urmare, este de dorit să se utilizeze secvențe a căror lungime este egală cu puterea numărului 2.
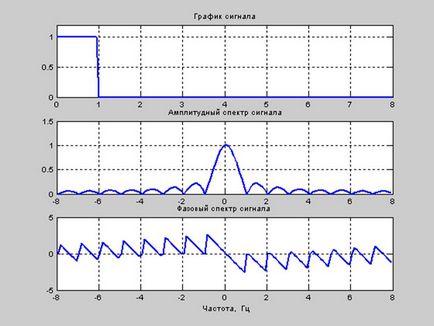
% Procedură pentru calcularea și plotarea spectrelor
% semnal utilizând funcția fft ()
N = 128; % număr de puncte
Ts = T / (N-1); % interval de eșantionare
t = 0: Ts: T; % interval de timp
tau = 2; % lățime puls
x = rectuls (t, tau); generarea unui impuls pătrat
subplotul (311), graficul (t, x), graficul semnalului de rețea%
set (gca, 'FontName', 'Arial Cyr', 'FontSize', 8)
titlu ("Program de semnal")
Fmax = 1 / Ts; % frecvență maximă
df = 1 / T; % rezoluție de frecvență
X = fft (x, N); % Semnal FFT
Xp = fftshift (X); % schimbare de frecvență
subplot (312), complot (f, abs (Xp) * Ts), grilă
set (gca, 'FontName', 'Arial Cyr', 'FontSize', 8)
titlu ("Semnalul spectrului de amplitudine")
% S = sinc (f * tau / 2) * tau / 2; % Transformare Fourier a semnalului
subplot (313), grafic (f, unghi (Xp)), grilă
set (gca, 'FontName', 'Arial Cyr', 'FontSize', 8)
xlabel ("Frecvență, Hz")
titlu ("Semnal de fază de spectru")
Analiza sistemelor liniare discrete
y = conv (x, h) - calculează convoluția secvențelor x și h. Cu convoluție, se calculează semnalul de ieșire al sistemului discret y cu răspunsul la impuls h și semnalul de intrare x în condiții inițiale zero.
Comanda conv poate fi de asemenea folosita pentru multiplicarea polinomilor, conv (a, b) este produsul polinomilor reprezentati de vectorii coeficientilor a si b.
Funcția de transfer a unui sistem discret
este reprezentat în MATLAB de vectorii coeficienților polinomilor numitorului și numitorului
Comenzile "dstep" și "dimpulse" calculează răspunsul tranzitoriu și impuls al sistemului respectiv
»Num = [10 0]; den = [1 -0,6 0,07];