Un nod de coș de coordonate este orice punct care se află la intersecția liniilor verticale și orizontale ale acestei rețele.
unde n este numărul de noduri din interiorul unui poligon dat, k este numărul de noduri care se află la limita lui (noduri de graniță).
Luați în considerare un triunghi obișnuit pe o rețea și încercați să marcați nodurile interne și limitate.
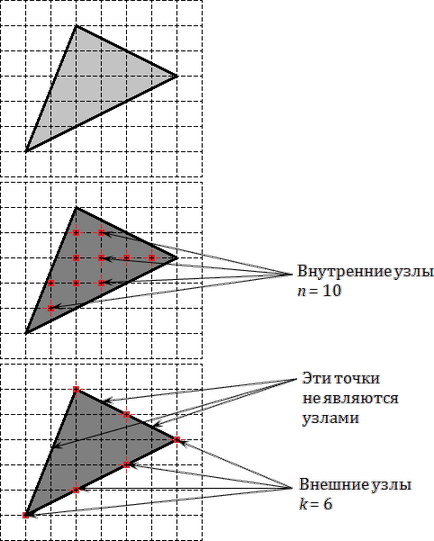
Prima imagine prezintă un triunghi obișnuit. Pe al doilea, nodurile sale interne sunt marcate, numărul lor fiind n = 10. A treia imagine prezintă nodurile situate la margine, există doar k = 6 dintre ele.
Limita unui poligon este o linie închisă închisă ce intersectează grilă de coordonate în multe puncte.
Găsiți zona triunghiului dacă dimensiunea celulei este de 1 x 1 cm:
Soluția
Mai întâi, marchează nodurile care se află în interiorul triunghiului și, de asemenea, la limita lui:
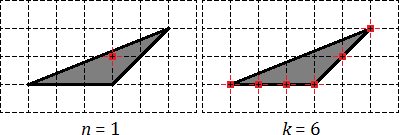
Se pare că nodul intern este unul singur: n = 1. Nodurile de graniță sunt de câte șase: trei coincid cu vârfurile triunghiului, iar altele trei se află pe laturi. Total k = 6.
Acum, luați în considerare zona conform formulei:
sarcină
Găsiți suprafața patrulaterului reprezentat pe hârtie în carouri cu o dimensiune a celulei de 1 cm pe 1 cm. Dați răspunsul în centimetri pătrați.

Soluția
Din nou, marchează nodurile interne și limitate. Nodurile interne sunt toate n = 2. Nodurile de graniță: k = 7, din care 4 sunt vârfurile patrulaterului și 3 mai sunt situate pe laturi.
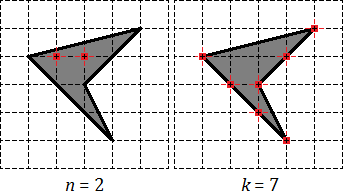
Rămâne să înlocuiți numerele n și k în formulele de zonă: