Concentrația electronilor n în banda de conducție și concentrația găurilor p în banda de valență pot fi reprezentate de următoarele expresii generale:
În analiza cuantică-mecanică sa stabilit că
unde h este constanta lui Planck; și sunt masele efective de electroni și găuri.
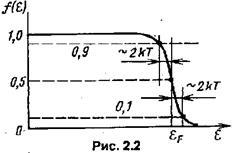
Funcția de probabilitate f (e) din (2.1) și (2.2) este determinată de formula
care se numește funcția de distribuție Fermi-Dirac. În această funcție k este constanta Boltzmann, T este temperatura absolută și a este energia nivelului Fermi. Evident, când. Prin urmare, formal, nivelul Fermi este un nivel, probabilitatea de a găsi un electron la care este de 0,5 (Figura 2.2). La T> 0 K, funcția are o scădere lină, dar rapidă, aproximativ în intervalul de energie ± 2 kT, în apropierea nivelului. La temperatura camerei (T = 300 K), kT = 0,026 eV, adică ± 2kT = ± 0,052 eV, care este mult mai mică, formând unitățile de electroni volți. Probabilitatea la. și când.
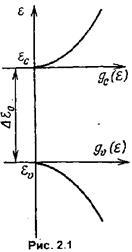
Funcția de distribuție trebuie să fie "legată" de diagrama de zonă a semiconductorului. De regulă, trebuie să știți unde este nivelul Fermi. In mod obisnuit semi-crestează în banda interzisă este: un semiconductor de tip n - la „distanță» >> 2KT din partea inferioară a benzii de conducție și în p-semiconductor - >> distanța banda de valență 2kTot și în Eq (2.5) se poate neglija unitatea în numitor; funcția de distribuție Fermi-Dirac reduce aproximativ la funcția de distribuție Maxwell-Boltzmann:
Semiconductorii pentru care funcția de distribuție Maxwell-Boltzmann este validă sunt numite nondegenerate. Acestea se caracterizează prin faptul că numărul particulelor este mult mai mic decât numărul de state permise. În cazul în care stratul semiconductor este numit Fermi-doc în gama 2KT în apropierea limitelor zonă sau în aceste zone, ar trebui să utilizați numai o funcție de Fermi-DIR-ka, și starea semiconductorului devine degenerat.
Formulele (2.7) și (2.8) sunt universale, deoarece sunt aplicabile la calculul concentrațiilor în orice tip de semiconductor: intrinsecă (tip i) și impuritate (tipuri n și p). Coeficienții u ar trebui interpretați ca un număr efectiv de state situate la limitele benzilor (nivele și care sunt incluse doar în formule). Valorile pentru siliciu și germaniu sunt de aproximativ 10 19 cm -3.
Formulele (2.7) și (2.8) ar trebui de asemenea înțelese ca o reflectare a relației dintre concentrație (numărul de purtători) și nivelul Fermi. Dacă valoarea este cunoscută, atunci putem calcula concentrațiile n și p corespunzătoare acestei valori. Dacă concentrația n (sau p) este cunoscută, atunci putem calcula valoarea corespunzătoare. În acest caz, formula este obținută de la (2.7) sau (2.8), dar rezultatul calculului ar trebui să se dovedească în mod natural ca fiind același:
Același rezultat este o consecință a legăturii existente între valorile concentrațiilor n și p. și anume conexiunea dintre numărul total de purtători din banda de conducție și banda de valență. Luați în considerare această relație.
Folosind (2.7) și (2.8), găsim produsul de concentrații:
Deoarece lățimea decalajului benzii
Aplicăm (2.10) un semiconductor adecvat (pur, pur), în care concentrația de electroni și găuri este aceeași. Obținem formula
care poate fi utilizat pentru a calcula concentrațiile purtătoarelor într-un semiconductor intrinsec fără a cunoaște poziția nivelului Fermi:
sau transformarea formulei (2.10) în formular
Semnificația acestei relații este că o creștere a concentrației particulelor cu un singur semn de încărcare este însoțită de o scădere a concentrației particulelor cu un semn diferit. O astfel de dependență se datorează faptului că, atunci când concentrația de electroni n crește, de exemplu, probabilitatea de recombinare a purtătorilor crește în mod proporțional, în urma căreia densitatea găurii p scade proporțional.
Calculul prin formula (2.12) oferă următoarele valori. pentru Ge, 2,4 10 13 cm-3; pentru Si, 1,45 10 10 cm-3; pentru GaAs este 1,79 10 6 cm -3. Creșterea lățimii benzii interzise de siliciu comparativ cu germaniul numai 1,12 / 0,66 = 1,7 ori a condus la o scădere a concentrației purtătorilor intrinseci cu aproximativ 10 3 ori.