1. O scurtă teorie
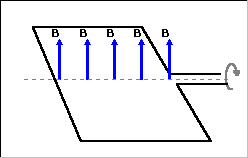
Conform legea inducției electromagnetice, prin schimbarea fluxului magnetic F penetrează circuitul conductor (bobina), apare fluxul de inducție EMF depinde de rata de schimbare
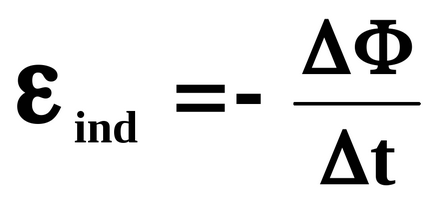
Fluxul magnetic printr-un contur plat al zonei S este cantitatea
unde B este modulul vectorului magnetic de inducție, este unghiul dintre vector

Dacă cadrul dreptunghiular planar al zonei S se rotește uniform cu o frecvență f de revoluție pe secundă într-un câmp magnetic omogen cu inducție

În consecință, o tensiune alternativă egală cu
Amplitudinea acestei tensiuni este proporțională cu viteza de rotație a cadrului. Un astfel de cadru, care se rotește într-un câmp magnetic, este un model al unui alternator. Dacă cablurile cadrului sunt conectate la un dispozitiv special de comutare (colector), se poate obține un generator de curent continuu.
2. Investigarea alternatorului
Modelul de computer vă permite să explorați anumite caracteristici ale alternatorului. Pentru a seta valorile de inducție B și frecvența f. ca de obicei, sunt utilizate bare de selecție. Pentru a seta zona dreptunghiulară a lui S, trebuie mai întâi să mutați cursorul în partea de sus a colțului cadrului astfel încât cursorul să pară o mână. Apoi, apăsați butonul stâng al mouse-ului (degetele mâinii vor fi comprimate pe cursor), în timp ce mutați butonul mouse-ului, mutați vârful colțului în locația dorită, controlați valorile setate de S. în fereastră și eliberând butonul.
Controlul asignării 1
Acum trebuie să urmați alegerea instructorului de sarcină de testare 1. Valorile fluxului magnetic ar trebui să fie înregistrate ținând cont de direcția sa față de planul normal față de planul cadrului. Cu valori pozitive, acesta pătrunde în direcția normală față de planul cadrului, cu valori negative, în direcția opusă. Rezultatele trebuie înregistrate într-un notebook de laborator.
Circuit pătrat plat, a cărui suprafață este S = 118 cm2. se rotește cu o frecvență f = 2 rev / sec într-un câmp magnetic omogen cu inducție B = 0,2 T. Determinați fluxul magnetic . piercing contour în cazul în care normală la planul său face un unghi = 30 ° cu linii de câmp.
Pentru a determina cât de mult timp va varia în fluxurile magnetice penetrante rotitor cu frecvența f = 2 rot / sec cadru dreptunghiular la două poziții în raport cu direcția câmpului magnetic B. colțurilor respective 1 = 0o și 2 = 30 ° între perpendiculară pe planul cadru și vector B.
Într-un câmp magnetic omogen, a cărui inducție este egală cu B = 0,2 T. se rotește cu o frecvență f = 2 RPM cadru pătrat, suprafața S = 100 cm2. Determinați fluxul magnetic . atunci când planul obișnuit față de planul său face un unghi = 45 ° cu direcția câmpului magnetic.
Un cadru dreptunghiular a cărui suprafață este S = 50 cm2. se rotește într-un câmp magnetic uniform, făcând 20 rev / sec. Axa de rotație se află în planul cadrului în mijlocul a două laturi înguste opuse ale cadrului și perpendicular pe liniile de forță ale câmpului magnetic. Inducerea câmpului magnetic este egală cu B = 0,1 T.
1) fluxul magnetic . perforarea cadrului, pentru momentele t = 0,1; 0,2; 0,3; 0,4 secunde;
2) valoarea maximă a fluxului magnetic .
Un contur plat dreptunghiular a cărui suprafață este S = 118 cm2. se rotește cu o frecvență f = 2 rev / sec într-un câmp magnetic omogen cu inducție B = 0,1 T. Determinați fluxul magnetic . piercing contour în cazul în care normală la planul său face un unghi = 30 ° cu linii de câmp.
Pentru a determina cât de mult timp va varia în fluxurile magnetice penetrante rotitor cu frecvența f = 2 rot / sec cadru dreptunghiular la două poziții în raport cu direcția câmpului magnetic B. colțurilor respective 1 = 0o și 45o 2 = între normala la planul cadrului și vector B.
Într-un câmp magnetic omogen, a cărui inducție este egală cu B = 0,1 T. se rotește cu o frecvență f = 2 RPM cadru dreptunghiular, suprafața S = 94 cm2. Determinați fluxul magnetic . atunci când planul obișnuit față de planul său face un unghi = 45 ° cu direcția câmpului magnetic.
Un cadru dreptunghiular a cărui suprafață este S = 100 cm2. se rotește într-un câmp magnetic uniform, făcând 20 rev / sec. Axa de rotație se află în planul cadrului în mijlocul a două laturi înguste opuse ale cadrului și perpendicular pe liniile de forță ale câmpului magnetic. Inducerea câmpului magnetic este egală cu B = 0,1 T.
1) fluxul magnetic . perforarea cadrului, pentru momentele t = 0,1; 0,2; 0,3; 0,4 secunde;
2) valoarea maximă a fluxului magnetic .
Un contur plat dreptunghiular a cărui suprafață este S = 79 cm2. se rotește cu o frecvență f = 2 rpm într-un câmp magnetic uniform cu inducție B = 0,15 T. Determinați fluxul magnetic . piercing contour în cazul în care normală la planul său face un unghi = 30 ° cu linii de câmp.
Pentru a determina cât de mult timp va varia în fluxurile magnetice penetrante rotitor cu frecvența f = 2 rot / sec cadru dreptunghiular la două poziții în raport cu direcția câmpului magnetic B. colțurilor respective 1 = 10o și 2 = 30 ° între perpendiculară pe planul cadru și vector B.
Un cadru dreptunghiular a cărui suprafață este S = 100 cm2. se rotește într-un câmp magnetic uniform, făcând 10 rev / sec. Axa de rotație se află în planul cadrului în mijlocul a două laturi laterale opuse ale cadrului și perpendicular pe liniile de forță ale câmpului magnetic. Inducerea câmpului magnetic este egală cu B = 0,2 T.
1) fluxul magnetic . perforarea cadrului, pentru momentele t = 0,05; 0,1; 0,15; 0,2 secunde;
2) valoarea maximă a fluxului magnetic .
Un cadru dreptunghiular a cărui suprafață este S = 100 cm2. se rotește uniform într-un câmp magnetic uniform, făcând 10 rev / sec. Axa de rotație se află în planul cadrului în mijlocul a două laturi laterale opuse ale cadrului și perpendicular pe liniile de forță ale câmpului magnetic, inducția cărora este egală cu B = 0,15 T. La momentul t = 0, planul cadrului este perpendicular pe vectorul de inducție.
1) fluxul magnetic . perforarea cadrului, pentru momentele t = 0,1; 0,2; 0,3; 0,4 secunde;
2) valoarea maximă a fluxului magnetic .