Numele vine de la grec. λημνίσκος - bandă, bandaj. În Grecia antică, "lemniscatul" a fost numit un arc, cu care o coroană a fost atașată de capul câștigătorului în jocuri sportive. Acest tip de lemniscat este numit după matematicianul elvețian Jacob Bernoulli. care și-a inițiat studiul.
Luați în considerare cel mai simplu caz: dacă distanța dintre focuri este de 2 c. acestea sunt situate pe axa OX. iar originea coordonatelor împarte segmentul între ele în jumătate, atunci următoarele ecuații dau un lemniscat:
Focarele lemniscatului sunt F1 (-c; 0) (-c; 0)> și F2 (c; 0) (c; 0)>. Luăm un punct arbitrar M (x; y). Produsul distanțelor de la focuri până la punctul M este
și prin definiție este c 2>:
Strângem ambele părți ale ecuației:
Deschidem parantezele din stânga:
Deschideți brațele și rotiți noul pătrat al sumei:
Luăm factorul și transferul comun:
Apoi putem face înlocuirea a 2 = 2 c 2 = 2c>. deși acest lucru nu este necesar:
În acest caz, a este raza cercului care descrie lemniscatul.
După efectuarea transformărilor simple, putem obține o ecuație explicită: y = ± c 4 + 4 x 2 c 2 - x 2 - c 2 + 4x ^ c ^ >> - x ^ -c ^ >>>
Strângem într-un pătrat și deschidem parantezele:
Îți aducem aminte
Luând rădăcina și aruncând varianta cu cel de-al doilea summit negativ, obținem:
unde varianta pozitivă definește jumătatea superioară a lemniscatului, negativul - jumătatea inferioară.
(ρ 2 cos 2 φ + ρ 2 sin 2 φ) 2 = 2 c 2 (ρ 2 cos 2 φ - ρ 2 sin 2 φ) \ rho ^ \ cos ^ \ varphi + \ rho ^ \ sin ^ \ varphi ^ = 2c ^ \ rho ^ \ cos ^ \ varphi - \ rho ^ \ sin ^ \ varphi>
Noi folosim încă o identitate: cos 2 α - sin 2 α = c o s 2 α \ alpha - \ sin ^ \ alpha = cos2 \ alpha>:
Ca și în cazul unui sistem rectangular, putem înlocui un 2 = 2 c 2 = 2c>:
Densitatea punctelor curbei pentru variația uniformă a parametrului
Aceasta este singura variantă a parametrizării raționale a curbei. Ecuația descrie complet curba când parametrul trece prin întreaga linie reală. de la - ∞ la + ∞. În acest caz, atunci când parametrul tinde să - ∞. punctul de curbă tinde să (0; 0) de la al doilea trimestru de coordonate. și când parametrul are tendința de a + ∞. apoi - de la al patrulea. Distribuția punctelor, care dă o ecuație parametrică, când se modifică parametrul cu un pas fix este prezentată în figură.
Ecuația lemniscată în sistemul polar
substituiți în formulele pentru tranziția la sistemul de coordonate polare x = ρ cos φ φ. y = ρ sin φ. ridicat în pătrat:
Luați în considerare prima ecuație:
x 2 = 2 c 2 cos 2 φ cos 2 φ = 2c ^ \ cos 2 \ varphi \ cos ^ \ varphi>
Extragem rădăcina de pe ambele părți ale ecuației:
Dacă înlocuim p 2 = tg (π 4 - φ) = \ operatorname \ left (> - \ varphi \ right)>. atunci obținem expresia dorită pentru x:
Pentru a defini o lemniscată cu două puncte arbitrare, este posibil să nu derivăm din nou ecuația, ci să determinăm transformarea coordonatelor la care lungimea focală veche (dată) devine una nouă și să acționăm asupra ecuațiilor prezentate prin această transformare.
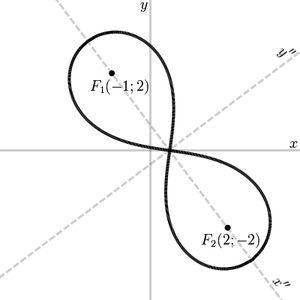
Fie, de exemplu, F 1 (- 1; 2). F 2 (2; -2) (-1; 2); F; (2; -2) sunt foci.
Există un sistem de coordonate dreptunghiular (în figură, x "O y"), în care ecuația lemniscată are forma
Este necesar să se determine transformarea sistemului de coordonate care ia x O y la x "O y". Această transformare se realizează în două etape: transferul paralel și rotația.
După mutarea sistemului de coordonate, acesta trebuie rotit într-un unghi. Pentru a determina unghiul, vom găsi mai întâi distanța dintre focare:
Acum, din motive geometrice, găsim sinusul și cosinusul unghiului pantă F 1 F 2 F_> k O X:
Combinând ambele transformări, obținem formule finite de tranziție:
Pentru a obține ecuația în sistemul de coordonate standard, substituim aceste relații în ecuația inițială a curbei:
x 2 + 2 x 2 + 2 x 2 - 2 x 3 + 5 x 2 - 4 x - 3 y 2 - 12 y + 15 16 = 0 + y ^ + 24xy-2xy + 2x ^ y ^ -2x ^ + 5x ^ -4x-3y ^ -12y +> = 0>
Această ecuație dă un lemniscat cu focare F 1 (- 1; 2). F 2 (2; -2) (-1; 2), \, F_ (2; -2)> în sistemul standard de coordonate dreptunghiulare.
Cu ajutorul secantelor (metoda lui Maclaurin)
Se construiește un cerc de rază c 2 >>> cu centrul la una din focare. De la mijlocul O al segmentului focal, se construiește o secțiune arbitrară O P S (P și S sunt punctele de intersecție cu cercul) și pe aceasta segmentele O M 1 și O M 2 sunt așezate pe ambele părți. egal cu coarda P S. Puncte M 1>. M 2> lieniscatele se află pe diferite bucle.
Metode de articulare
Opțiunea unu
Două puncte sunt alese în avion - A și B - viitoarele focare ale lemniscatei. Există o construcție specială de trei îmbinate pe balamalele segmentelor, astfel încât linia rezultată se poate îndoi liber în două locuri (punctele de întindere - C și D). În acest caz, este necesar să se respecte proporțiile segmentelor: A C = B D = A B 2. C D = A B >>, \ CD = AB>. Marginile liniei sunt atașate la focuri. În cazul unei rotații neparale a segmentelor din jurul focarelor, mijlocul segmentului central va descrie lemniscatul lui Bernoulli.
Opțiunea a doua
În această variantă, lemniscatul este construit de-a lungul punctului focal, iar punctul dublu - A și O, respectiv. Există aproape aceeași construcție a balamalelor ca în versiunea anterioară, dar segmentul O C atașat la punctul dublu este conectat nu la capătul centrului BD. dar cu mijlocul său. Proporțiile sunt de asemenea diferite: B C = C D = O C = A O 2. A B = A O >>, \ AB = AO>.
Construirea unei lemniscate cu ajutorul secantelor