Fiecare cifră are propriile cerințe de reglementare, exprimând particularitățile încheierii logice. Și anume:
1. O premisă mare ar trebui să fie o propunere generală.
2. O premisă mai mică ar trebui să fie afirmativă.
1. O premisă mare ar trebui să fie o propunere generală.
2. Și unul dintre premise este o propunere negativă. Concluzia este o judecată negativă (E, O).
1. O premisă mai mică este o propoziție afirmativă.
2. Concluzia este o propunere particulară (/, 0).
Confirmarea generală nu dă. După cum sa menționat deja, acesta este cel mai puțin informativ.
Fiecare figură își desfășoară propriile sarcini cognitive specifice:
• Prima cifră este indispensabilă pentru construirea dovezilor;
• al doilea este preferabil pentru respingere;
• A treia contribuie la evitarea generalizărilor rapide.
Cu toate acestea, cel mai adesea în practica noastră de viață trebuie să dovedim ceva, să ne justificăm punctul de vedere. Și dovezile evidente sunt doar dovezi ale primei cifre (se bazează pe axiomul silogismului). Prin urmare, o mare importanță este posibilitatea reducerii silogismului la prima figură. Acest lucru, în primul rând. Și în al doilea rând, prin reducere la prima cifră devine clar ca modurile corecte ale celorlalte figuri, pentru că o dată folosind axioma silogismului înțelegem dovada modurilor de prima cifră, este, de asemenea, convins de corectitudinea modurilor de celelalte figuri, prima cifră Modus echivalentă. Cum are loc reducerea silogismelor? Prin trimiterea pachetelor (desigur, dacă este posibil). De exemplu, luați silogismul celei de-a doua figuri:
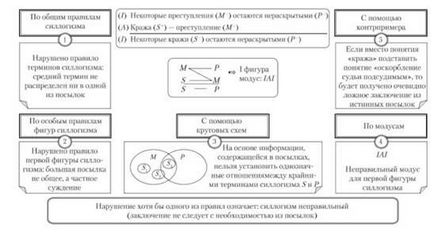
(£) "Cine este prea frică de ură (P),
Napoleon (5) nu era prea frică de ură (P).
Pentru a obține prima figură a silogismului, trebuie să desenezi o parcelă mare, respectând regulile de tratament. Deoarece această premisă este o hotărâre negativă, ambii termeni (M și P) sunt distribuiți, deci un recurs pur este posibil:
nu prea frică de ură (P). (A) Napoleon (5) a reușit să controleze (M).
(£) Napoleon (5) nu era prea frică de ură (P).
În mod similar se aplică și altor figuri. În cea de-a treia figură, parcela mai mică este inversată, iar cea de-a patra, ambele.
Cuvântul "algoritm" vine de la lat. Algorithmi - ortografia Muhammad al-Khwarizmi (787-850) - un matematician remarcabil al Orientului medieval și este rețeta exactă, care definește o secvență de acțiuni care vor asigura rezultatul dorit din datele brute. Aplicată la silogism, sunt posibile acțiuni algoritmice. Într-o formă clară, ele sunt reflectate în Fig. 6.2.
Luați în considerare acest lucru pentru un exemplu specific.
"Totul în domeniul minții este o concluzie." (G. Hegel). PKS este o concluzie. IIKS aparține sferei minții.
În acest argument, din premisele adevărate, se obține o adevărată concluzie care încurajează și menține o încredere subiectivă în logicitatea raționamentului. Să vedem dacă este așa.
1. Constituim structura silogismului:
• în închisoare găsiți și lăsați subiectul (5) - mai mici termenul silogismului ( „PKC“) și predicatul (P) -Large termenul ( „ceea ce face parte din sfera minții“) (!);
• le găsim și le desemnează în incintă;
• indicați termenul de mijloc (M) - "inferență"). Tot ce aparține domeniului minții (P) este o deducere
PKS (5) se referă la sfera minții este (P);
a) o premisă mare (include predicatul închisorii):

"Tot ceea ce are legătură cu sfera rațiunii (N) este o concluzie (P)";
b) o premisă mai mică (include subiectul încheierii): "PCC (5) se referă la sfera rațiunii (M)"; Suntem convinși că silogismul este înregistrat în forma standard, că în primul rând o premisă mare. Standard Record silogism oferă confortul de analiză logică a silogismului, și în multe cazuri, pentru a evita erorile comune (de exemplu, în determinarea formei și modus). În acest caz, silogismul este înregistrat în forma standard;
• În cazul înregistrării non-standard, ar fi necesar să se schimbe parcelele în anumite locuri (a le aduce în vedere standard).
2. Determinați cifra PKC: a doua cifră.
(A) Tot ceea ce este legat de sfera rațiunii (P) este o concluzie (M).
(A) PKS (5) se referă la sfera minții este (P).
4. Noi stabilim distribuția termenilor:
(A) Tot ce are legătură cu sfera rațiunii (P +) este o concluzie (M
(l) PKC (5+) - inferență (M-).
(l) PKS (5+) se referă la sfera rațiunii (P
(Eroare deja vizibilă - termenul mediu nu este distribuit în niciuna dintre colete.)
• În conformitate cu regulile generale ale PCU, Termenii de utilizare.
1. Trebuie să existe trei termeni în silogism. - Exista.
2. Termenul mediu ar trebui să fie distribuit cel puțin într-una din colete. - Încălcată (termenul mediu nu este distribuit în niciuna din parcele).
3. Termenul, nealocat pe parcelă, nu trebuie distribuit în custodie. - Observată.
1. Cel puțin una dintre premise trebuie să fie o propunere generală. "Ambele sunt comune."
2. Cel puțin unul dintre locații trebuie să fie afirmativ. - Ambele sunt afirmative.
3. Dacă există o parcelă privată, concluzia trebuie să fie privată. Hci parcele private.
4. Dacă există o premisă negativă, concluzia trebuie să fie negativă. - Nu există o premisă negativă.
Regulile parcelelor sunt respectate.
1. O premisă mare ar trebui să fie o propunere generală. - Așa este.
2. Unul dintre premise trebuie să fie negativ. - E rupt.
• Moduri: ALA este modul greșit pentru a doua cifră.
- luăm în considerare informații numai din parcele (concluzia nu este luată în considerare);
- Începem să construim cu o premisă mai mare;
- pentru comoditate, formalizăm sediul: "Tot P este M",
Construcția schemelor este mai bine să începem cu o premisă mai mare: "Tot P este M".
Adăugați la informațiile despre imagine din parcela mai mică: "Tot S este M".
După cum vedem, este imposibil să se stabilească relații lipsite de ambiguități între termenii S și P extreme. • Cu ajutorul unui exemplu de proba.
"Toți studenții (P) sunt studenți (M)". <• Исс школьники (5) учащиеся (Л/)". "Все школьники (5) — студенты (Р)".
Răzbunarea prin același sistem, din premisele adevărate, ajungem la o concluzie falsă. Acest lucru indică faptul că o astfel de modalitate de comunicare a gândurilor nu este logic necesară.
Concluzie: Syllogismul este greșit (concluzia nu este însoțită de nevoia de parcele).
Inferența este o operație logică cu judecăți, permițându-vă să obțineți un câștig de cunoștințe fără a se îndrepta către surse suplimentare de informații. Gradul veridic garantat al concluziilor este asigurat numai prin deducere.
În direcția mișcării gândirii, raționamentul este împărțit în deductiv, inductiv și transductiv.
Logica modernă împarte inferențele prin natura conexiunii dintre premise și concluzii la demonstrative și plauzibile.
Rezultatele demonstrative (deductive) sunt împărțite în două mari grupuri: silogismul și raționamentul logicii judecăților. La rândul lor, silogismul este împărțit în imediată și indirectă.
Trebuie amintit faptul că caracterul logic de bază al inferenței este corectitudinea logică.