Să luăm în considerare semnificația geometrică fundamentală a integrala dublă. Presupunem că funcția există în fiecare punct al planului.
Din punct de vedere geometric, funcția a două variabile definește o anumită suprafață în spațiul tridimensional. Pentru claritate, presupunem asta. adică suprafața este situată deasupra planului.
Apoi integralele duble sunt numeric egale cu volumul unei fascicule cilindrice:
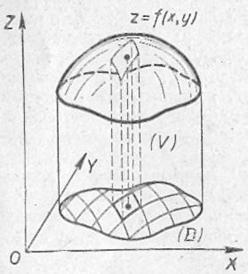
Ce este un bar cilindric, cred, toată lumea înțelege din desen. O figură plată (umbrită în desen) se află în întregime în plan și bara este delimitată de regiune de dedesubt. Deasupra fasciculului este doar delimitată de suprafață. care este un astfel de capac. Din punct de vedere figurativ, o regiune plată taie acest capac de pe suprafața sa prin razele sale perpendiculare.
În plus, voi explica semnificația geometrică din Exemplul 1. În el am considerat integralele duble. iar domeniul de integrare a avut următoarea formă:
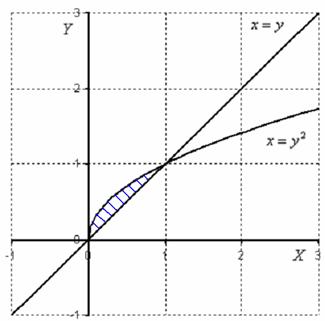
Integratul dă avionul în spațiu. De la origine, perpendicular pe ecranul monitorului, trageți mental săgeata axei. În acest exemplu, planul este situat în spațiul de deasupra regiunii. astfel încât volumul corpului sa dovedit a fi pozitiv :. Poate că nu toată lumea înțelege până la capăt ce volum se vorbește: de la granița regiunii direcționează razele spre tine. Aceste raze vor tăia o bucată din avion. care se află deasupra zonei.
Integralul dublu poate fi de asemenea negativ, în astfel de cazuri, graficul funcțional complet (sau cel mai mult) se află sub regiune. Acesta este și volumul corpului, doar cu un semn minus, deoarece suprafața totală (sau cea mai mare parte a acesteia) se află sub planul coordonatelor.
Îmi cer scuze, până când am găsit un program de construire a desenelor 3D care ar fi potrivit pentru mine, a trebuit să explic pe degetele mele.
Cu toate acestea, în practică aproape întotdeauna există probleme la calcularea formală a integralelor duble, prin urmare vom continua să îmbunătățim tehnica de calcul:
Calculați integramentul dublu
.
Soluție: Desenați zona de integrare pe desen:
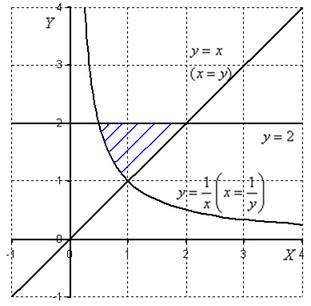
După ce desenul este executat corect și zona de integrare este corect localizată, este timpul să dați seama de ordinea bypass-ului.
Conform primei metode de by-pass, regiunea va trebui împărțită în două părți și vor trebui calculate următoarele integrale:
Entuziasmul, sincer vorbind, nu este de ajuns. Să analizăm, nu este mai ușor să folosiți a doua cale în jurul zonei? Trecem la funcțiile inverse, tranziția este elementară:
Ordinea zonei de bypass:
Pai, o alta problema. Și din nou, rețineți că în integrarea interioară integrarea este efectuată cu "X", astfel încât constanta poate fi scoasă imediat la integralele exterioare
1) Am găsit integralele interioare:
Totuși, înlocuirea limitelor de integrare, uneori, pare ciudat. Începând cu site-ul "X", am stabilit limita superioară a integrării. atunci, în loc de "X", limita inferioară a integrării a fost înlocuită. Fii atent cu permutarea!
2) Rezultatul paragrafului anterior este înlocuit în integralul exterior, în timp ce noi nu uităm. care este deja acolo:
Pentru instruire, puteți încerca să calculați integralele duble într-un mod mai puțin rațional :. Rezultatele ar trebui să coincidă.
Calculați integramentul dublu
.
Acesta este un exemplu de auto-decizie. Construiți o zonă și analizați ce cale de ocolire a zonei este mai profitabil de utilizat. Completați soluția și răspundeți la sfârșitul lecției.
Noi complicăm problema, acum funcția integrand este o sumă. Să luăm în considerare încă două exemple, în care mă voi concentra asupra calculului unui integral, tipic și eficace pentru integrale multiple:
Calculați integramentul dublu
.
Soluție: Mai întâi, luăm în considerare ceea ce nu trebuie să facem - în acest caz nu ar trebui să folosim proprietățile de linearitate ale integrala multiplă și să o reprezentăm sub forma:
De ce? Calculele vor crește considerabil!
Soluția, ca de obicei, începe cu construirea domeniului de integrare:
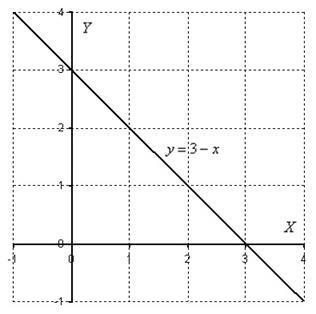
Zona este necomplicată, nici măcar nu o voi expune. În acest exemplu, așa cum este ușor de văzut, ordinea integrării nu are nici un înțeles special, deci vom alege prima variantă obișnuită de eludare a regiunii:
Aici, spre deosebire de cele două exemple anterioare, nimic nu poate fi scos din integramentul interior, deoarece umplerea este suma.
Ne ocupăm din nou cu integratele repetate separat. Oh, și care doresc să vadă cum să se ocupe cu integralele repetate într-o singură linie, vă rugăm să vizitați pagina Soluții pentru matematici superioare și încărcați fișierul cu exemple de soluții multiple integralelor.
1) În primul rând, luăm integrala interioară:
Aș dori să mă ocup de câteva puncte importante. În primul rând, despre integrarea privată. Despre el am spus deja în detaliu în articolul Ecuații diferențiale în diferențiale complete. Pe scurt, repet: