<<Вычисли площади всех прямоугольников
Uite, în figură, un triunghi dreptunghiular >>
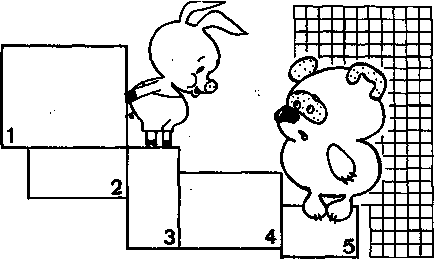
"Cum să determinăm zona unei figuri geometrice complexe?" - întreabă Pigletul Winnie the Pooh. Porcul explică: trebuie să divizăm figura geometrică în dreptunghiuri; În primul rând. Al doilea. 2) determinați aria fiecărui dreptunghi, apoi introduceți rezultatele în pătrate; 3) adăugați zona tuturor dreptunghiurilor și înregistrați rezultatul. Al treilea. În al patrulea rând. În al cincilea rând. (A se vedea). + + + + =. Și acum desenați o figură geometrică complexă și definiți zona ei. 2.
Imaginea 91 din prezentarea "Divertisment de geometrie"
Dimensiuni: 1037 x 625 pixeli, format: png. Pentru a descărca o fotografie gratuită pentru lecția de geometrie, faceți clic pe imagine cu butonul din dreapta al mouse-ului și faceți clic pe "Salvați imaginea ca". “. Pentru a afișa imagini în clasă, puteți descărca, de asemenea, prezentarea liberă „geometriya.ppt de divertisment“, în întregime, cu toate imaginile din zip-arhivă. Dimensiunea arhivei este de 4498 KB.
Prezentări înrudite
"Zona de figuri de geometrie" - figuri egale b). Teorema lui Pitagora. c). care va fi egală cu aria figurinei formată din figurile A și D. Zona paralelogramului. Zona triunghiului. Figurile cu zone egale sunt numite egale. Dintre figurile indicate în figură, indicați. Figurile egale au zone egale. Dreptunghi, triunghi, paralelogram.
"Optica geometrică" - Compoziție spectrală. Limita optică geometrică. Oglinda sferică. În spațiul gol, lumina se propagă rectiliniu (raze - linii drepte). Viteza luminii c = 300 000 000 m / s. F = R / 2 F - lungimea focală R - raza oglinzii. Reflecție în oglindă. De fapt, totul este mult mai complicat decât se gândea Newton.
"Corpuri geometrice" - II. Lungime. Piramida. În mediul înconjurător, multe obiecte au forma unui paralelipiped dreptunghiular. În funcție de forma lecției, diapozițiile pot fi folosite selectiv. Corpurile, limitate nu numai de suprafețe plane, sunt numite corpuri circulare. Testul pentru lecție poate fi folosit în cea de-a zecea formă în subiectul "Polyhedra".
"Simetria figurilor" - Transformarea cifrelor. Punctul P este simetric față de el în raport cu linia dreaptă c. Cuprins. Linia dreaptă a se numește axa de simetrie a figurii. Punctul O este presupus a fi simetric cu el însuși. Punctele M și M1 sunt simetrice în raport cu linia dreaptă c. C. Simetria, în greacă, înseamnă proporționalitate. Cum rămâne cu punctele M și M1?
"Volumele figurilor" - Orice corp geometric din spațiu este caracterizat de o cantitate numită VOLUM. Lăsați o prismă triunghiulară înclinată. Construim o secțiune perpendiculară pe marginea laterală (? BKC). 2) Completăm această prismă la paralelipipedul dreptunghiular ADECA1D1C1E1. 3) Am obținut două prize triunghiulare directe ADBA1D1B1 și BECB1E1C1.
"Simetria figurilor geometrice" - Hermann Weil. Atunci când frumusețea atrage, și entrains de cercetare. Dreptunghi. Colț nedevelopat. Rombomul are două axe de simetrie. Dreptunghiul are două axe de simetrie. Rombomul. Cuvântul "simetrie" în greacă înseamnă "identic în aranjarea părților". Triunghiul complet. Un triunghi isoscel are o axă de simetrie.
24 de prezentări despre geometrie