- Formarea de abilități și abilități în rezolvarea problemelor geometrice folosind teorema lui Pitagora.
- Dezvoltarea culturii grafice și a discursului matematic.
- Extindeți opiniile elevilor cu privire la aplicarea practică a teoremei pitagoreene, educația de mindfulness, purposefulness, organizare, responsabilitate, independență.
Motivația studenților: dependența de materialele studiate anterior; activități practice ale studenților
Principalele metode de predare: euristică, reproductivă, practică și cercetare
Forme de organizare a activităților educaționale: frontal, individual, independent, colectiv.
Întreținerea tehnică a lecției: computer, proiector multimedia, ecran, portrete ale matematicienilor.
I. Oral. Repetați materialul trecut (se utilizează proiector multimedia).
1. Ce triunghi este arătat în Figura 1?
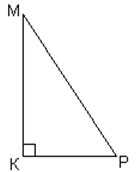
2. Denumiți picioarele și hypotenuse.
(MK și KR - picioarele, MP - hypotenuse).
3. Express cosM, cosP.
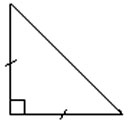
4. Care este triunghiul din Figura 2? Cum este interesant?
(Inversat, dreptunghiular, cu colțuri la baza de 45 °, poate fi completat la un pătrat cu o latură egală cu piciorul).
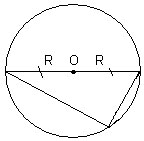
5. Care este triunghiul din Figura 3?
(Rectangular, O este centrul unui cerc.)
II. Discuția profesorului
Astăzi vă veți familiariza cu una dintre puținele teoreme ale geometriei pe care toți elevii o amintesc. Dar mai întâi vă voi spune despre matematicianul al cărui nume este denumit această teoremă.
- Băieți, știi ceva legat de numele lui Pitagora?
(Unii elevi pot formula teoria în sine sau celebra fraza: „pantaloni pitagoreice de pe toate laturile sunt egale“, sau vorbesc despre puzzle - joc „Pitagora“)
- Vom vorbi despre toate astea.
Vom scrie tema lecției: "Teorema Pitagora".
În manualele moderne, teorema este formulată după cum urmează: "Într-un triunghi dreptunghiular, pătratul hypotenusei este egal cu suma pătratelor picioarelor."
Să desenați un triunghi dreptunghiular (Figura 4) și scrieți această afirmație în notație:
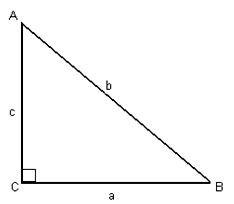
În timpul lui Pitagora, formularea teoremei a fost:
"Demonstrați faptul că pătratul construit pe ipoteza unui triunghi dreptunghic este egal cu suma pătratelor construite pe picioarele"
"Zona pătratului construită pe ipoteza unui triunghi dreptunghic este egală cu suma pătratelor pătrate construite pe picioarele ei."
Teorema lui Pythagoras are o istorie bogată. Se pare că cu mult înainte ca Pythagoras să fie cunoscut egiptenilor, babilonienilor, chinezilor și indienilor. Timp de opt secole î.Hr. teorema lui era bine cunoscută indienilor numit „regula de coarda“ și le-a folosit pentru a construi altare, care sunt sacre ordin de furnizare ar trebui să aibă o formă geometrică strictă, orientată în raport cu cele patru laturi ale orizontului.
Dovada lui Pitagora nu ne-a atins. În prezent, există peste o sută de dovezi diferite ale teoremei pitagoreene. Este posibil ca unul dintre ei să aparțină lui Pythagoras sau elevului său.
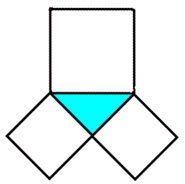
Probabil, faptul afirmat în teorema pitagoreană a fost inițial stabilit pentru triunghiurile dreptunghiulare isosceles (Figura 5)
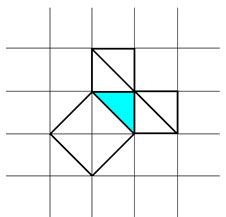
Un pătrat construit pe o hypotenuse conține patru triunghiuri, iar pe fiecare picior este construit un pătrat care conține două triunghiuri. Figura 6 arată că aria pătratului construită pe hypotenuse este egală cu suma pătratelor pătrate construite pe picioare.
- Uite, și aici sunt pantalonii pitagoreci în toate direcțiile sunt egale. " Aceste rime au fost inventate de studenți; a desenat desene animate teoremei pitagoreene. Aici, de exemplu, cum ar fi în figura 7.
III. Acum dovedim teorema
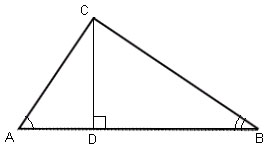
- Deci, să arătăm că în triunghiul drept, pătratul hypotenusei este egal cu suma pătratelor picioarelor. Desenați desenul (Figura 8) și scrieți dovada în notație.
(Folosind întrebări de bază, păstrez o înregistrare pe tablă, iar băieții sunt în notebook-urile mele).