Scurtă descriere a documentului:
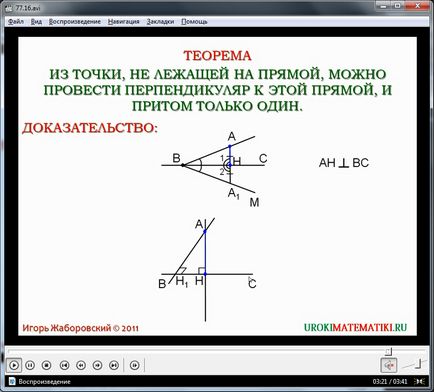
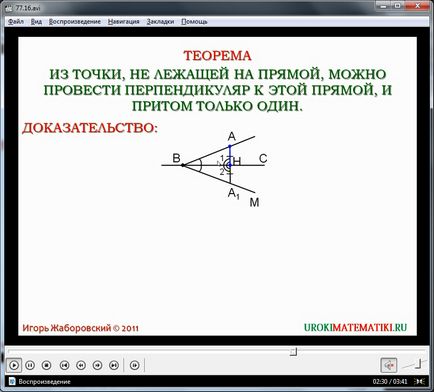
Apoi elevii sunt prezentați cu o dovadă a unei teoreme importante care va ajuta la rezolvarea multor probleme geometrice și va dovedi următoarele teoreme. Textul teoremei este afișat pe ecran și poate fi sugerat pentru scrierea în notebook-ul studentului. Dovada teoremei începe cu construirea liniei drepte BC și a punctului A care nu aparține liniei BC. Prima parte a probei este că un punct perpendicular pe linia dreaptă BC poate fi extras din punctul A. Pentru a demonstra această afirmație, mai întâi construim un unghi ∠ MWS, care este egal cu unghiul ∠ABC, construit de la începutul razei BC. Deoarece aceste unghiuri sunt egale, atunci când se suprapun coincid. Lățimile VA și VSAWS coincid de asemenea cu laturile VM și VS ale unghiului ∠ MVS. În acest caz, punctul A este suprapus pe punctul A1. Se marchează un punct H, care este intersecția segmentului AA1 și linia dreaptă BC. Această suprapunere poate fi interpretată ca inflexiunea modelului de-a lungul liniei drepte BC. Secțiunea AN care rezultă este perpendiculară pe linia dreaptă H. Și raza HA este aliniată cu raza HA1. Astfel ∠1 - unghiul de intersecție al segmentului de AN și direct soarele suprapus peste ∠2 - unghiul HA1 de intersecție a segmentului și Soare directe În acest caz, unghiurile ∠1 și ∠2 sunt adiacente. S-ar putea argumenta că fiecare linie a acestor unghiuri, deoarece suma unghiurilor adiacente este de 180 °, iar din moment ce se formează unghiurile de trecere, AN-ul este linia perpendiculară BC. Desemnarea liniilor drepte perpendiculare este indicată pe ecran cu un simbol special destinat pentru memorare.
A doua parte a probei este dedicată faptului că numai o perpendiculară pe BC poate fi trasă din punctul A. Pentru aceasta, o construcție suplimentară se face sub prima figură. Dovada este prin contradicție. Se presupune că din punctul A se pot desena mai multe linii drepte perpendiculare pe linia dreaptă BC. În figură se trasează o altă linie perpendiculară, cu excepția perpendicularului, care coboară din punctul A pe linia BC. Cu toate acestea, se pare că linia construită AN1 se va intersecta cu perpendicularul AN existent. Și acest lucru este imposibil, prin urmare, din punctul A se poate trasa o singură linie dreaptă perpendiculară pe BC - aceasta dovedește teorema.