unde δ Q i = δ Q 1 i + δ Q 2 i este cantitatea de căldură primită de corpul de lucru la două secțiuni izotermice la temperatura T i. Pentru a realiza un astfel de ciclu complex într-o manieră reversibilă, este necesar ca mediul de lucru să fie adus în contact termic cu multe rezervoare de căldură cu temperaturi T i. Raportul δ Q i / T i se numește căldură redusă. Formula obținută arată că căldura totală redusă în orice ciclu reversibil este zero. Această formulă ne permite să introducem o nouă cantitate fizică, care se numește entropie și este notată cu litera S (R. Clausius, 1865). Dacă sistemul termodinamic trece de la o stare de echilibru la alta, atunci entropia sa se schimbă. Diferența valorilor entropiei în două stări este egală cu căldura redusă primită de sistem în timpul unei tranziții inversibile de la o stare la alta.
În cazul reversibil adiabatic proces δ Q i = 0 și, prin urmare, entropia S rămâne neschimbată.
Expresia pentru schimbarea entropiei δS la trecerea unui sistem neizolat dintr-o stare de echilibru (1) într-o altă stare de echilibru (2) poate fi scrisă sub forma
Entropia este definită până la un termen constant, la fel ca, de exemplu, energia potențială a unui corp într-un câmp de forță. Sensul fizic este diferența δ S a entropiei în două stări ale sistemului. Pentru a determina schimbarea entropiei în cazul unei tranziții ireversibile a unui sistem de la o stare la alta, trebuie să apară un fel de proces reversibil care să conecteze stările inițiale și finale și să găsească căldura redusă obținută de sistem într-o astfel de tranziție.
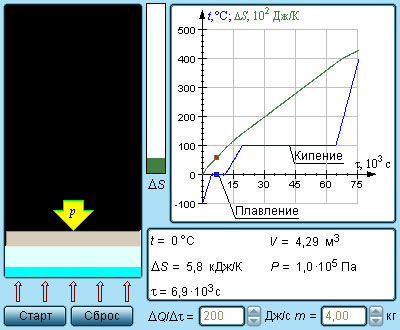
Modelul. Entropie și tranziții de fază
Fig. 3.12.4 ilustrează procesul ireversibil de extindere a gazului "în gol", în absența schimbului de căldură. Numai stările inițiale și finale ale gazului în acest proces sunt echilibru și pot fi reprezentate în diagramă (p. V). Punctele (a) și (b) care corespund acestor stări se află pe o izotermă. Pentru a calcula schimbarea δ S de entropie, putem considera o tranziție izotermică inversibilă de la (a) la (b). Deoarece sub o expansiune izotermică gazul primește o anumită cantitate de căldură din corpurile din jur, Q> 0. Se poate concluziona că pentru o expansiune ireversibilă a gazului entropia a crescut: δ S> 0.
Extinderea gazului în "gol". Schimbarea entropiei în cazul în care A = Q este lucrarea unui gaz sub expansiune izotermă reversibilă
Un alt exemplu al unui proces ireversibil este schimbul de căldură cu o diferență de temperatură finită. În Fig. Figura 3.12.5 prezintă două corpuri închise într-o coajă adiabatică. Temperaturile inițiale ale corpurilor T 1 și T 2
Transferul de căldură la o diferență de temperatură finită: a - starea inițială; b - starea finală a sistemului. Schimbarea entropiei δ S> 0
Creșterea entropiei este o proprietate comună a tuturor proceselor ireversibile apărute spontan în sistemele termodinamice izolate. În procesele reversibile din sistemele izolate, entropia nu se schimbă:
Această relație este, de obicei, numită legea entropiei crescânde.
În orice proces care apare în sistemele izolate termodinamice, entropia rămâne fie neschimbată, fie crește.
Astfel, entropia indică direcția proceselor spontane. Creșterea entropiei indică apropierea sistemului de starea echilibrului termodinamic. Într-o stare de echilibru, entropia preia o valoare maximă. Legea entropiei crescânde poate fi adoptată ca o altă formulare a celei de-a doua legi a termodinamicii.
În 1878, L. Boltzmann a dat o interpretare probabilistică a conceptului de entropie. El a propus să ia în considerare entropia ca măsură a tulburărilor statistice într-un sistem termodinamic închis. Toate procesele care au loc în mod spontan într-un sistem închis, aduce sistemul la o stare de echilibru, și însoțită de o creștere a entropiei, sunt îndreptate spre creșterea probabilității statului.
Orice stare a unui sistem macroscopic care conține un număr mare de particule poate fi realizată în mai multe moduri. Probabilitatea termodinamică W a unei stări de sistem este numărul de căi. care poate fi realizată o stare dată a unui sistem macroscopic sau numărul de micro-stații. realizarea acestei macrostate. Prin definiție, probabilitatea termodinamică este W >> 1.
De exemplu, dacă există 1 mol de gaz în vas, atunci este posibil un număr foarte mare de N moduri de plasare a moleculei de-a lungul celor două jumătăți ale vasului: unde este numărul Avogadro. Fiecare dintre ele este o microstat. Numai una dintre microstații corespunde cazului în care toate moleculele sunt asamblate într-o jumătate (de exemplu, dreapta) a vasului. Probabilitatea unui astfel de eveniment este practic zero. Cel mai mare număr de microstații corespunde stării de echilibru, în care moleculele sunt distribuite uniform pe întregul volum. Prin urmare, starea de echilibru este cea mai probabilă. Pe de altă parte, starea de echilibru este o stare a celei mai mari tulburări din sistemul termodinamic și o stare cu entropie maximă.
Potrivit lui Boltzmann, entropia S a sistemului și probabilitatea termodinamică W sunt legate după cum urmează:
unde k = 1,38 · 10 -23 J / K este constanta Boltzmann. Astfel, entropia este determinată de logaritmul numărului de microstații. cu ajutorul căruia se poate realiza această macrostată. În consecință, entropia poate fi privită ca o măsură a probabilității unei stări a unui sistem termodinamic.
Interpretarea probabilistică a celei de-a doua lege a termodinamicii permite o deviere spontană a sistemului de la starea echilibrului termodinamic. Astfel de abateri se numesc fluctuații. În sistemele care conțin un număr mare de particule, deviațiile semnificative de la starea de echilibru au o probabilitate extrem de scăzută.