Energia cinetică a sistemului este cantitatea scalară T, egală cu suma aritmetică a energiilor cinetice ale tuturor punctelor sistemului
Energia cinetică este o caracteristică atât a mișcării translaționale, cât și a celei de rotație a sistemului, astfel încât teorema privind schimbarea energiei cinetice este folosită în special în rezolvarea problemelor.
Dacă sistemul este alcătuit din mai multe corpuri, atunci energia cinetică este evident egală cu suma energiilor cinetice ale acestor corpuri:
Energia cinetică este scalară și mereu pozitivă.
Să găsim formulele pentru calcularea energiei cinetice a corpului în diferite cazuri de mișcare.
1. Mișcare progresivă. În acest caz, toate punctele corpului se mișcă cu viteze identice, egale cu viteza centrului mișcării în masă. Asta este, pentru orice punct
Astfel, energia cinetică a corpului cu mișcare de translație este egală cu jumătate din produsul masei corpului de către pătratul vitezei centrului de masă. Valoarea lui T nu depinde de direcția mișcării.
2. Mișcarea de rotație. Dacă corpul se rotește în jurul unei axe Oz (vezi Fig.46), atunci viteza oricărui punct. unde este distanța de la axa de rotație și w este viteza unghiulară a corpului. Înlocuind această valoare și luând multiplicatorii obișnuiți de bracket, obținem:
Valoarea în paranteză este momentul inerției corpului în raport cu axa z. Astfel, în sfârșit găsim:
adică energia cinetică a corpului pentru mișcarea de rotație este egală cu jumătate din produsul momentului de inerție al corpului față de axa de rotație de către pătratul vitezei sale unghiulare. Valoarea lui T nu depinde de direcția de rotație.
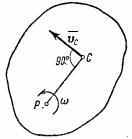
Atunci când corpul se rotește în jurul unui punct fix, energia cinetică este determinată ca (figura 47)
unde Ix. Iy. Iz sunt momente de inerție a corpului față de axele principale ale inerției x1. y1. z1 la punctul fix O; . , Este proiecția vectorului de viteză unghiulară pe aceste axe.
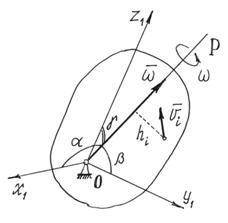
3. Mișcarea paralelă-plană. În această viteză mișcare SRI din toate punctele corpului în fiecare moment de distribuție Lena ca și în cazul în care corpul este rotit în jurul unei axe perpendiculare pe planul de mișcare și care trece prin centrul instantaneu de SKO creștere P (Fig.46). prin urmare
unde este momentul inerției corpului față de axa numită mai sus, w este viteza unghiulară a corpului. Valoarea din formula va fi variabilă, deoarece poziția centrului P se modifică odată cu mișcarea corpului. Introducem în schimb un moment constant de inerție, în raport cu axa care trece prin centrul masei C a corpului. Prin teorema lui Huygens, unde d = PC. Înlocuim această expresie. Având în vedere că punctul P este centrul instantaneu al vitezelor și, în consecință, unde este viteza centrului de masă C, găsim în cele din urmă:
Prin urmare, atunci când mișcarea plan paralelă energia cinetică a corp lic egală cu energia mișcării de translație cu centrul vitezei stratului-zhennoy energie skineticheskoy masa de mișcare de rotație în jurul centrului de masă.
4) Pentru cel mai general caz al mișcării unui sistem material, energia cinetică ajută la calcularea teoremei lui Koenig.
Luați în considerare mișcarea sistemului material ca sumă a două mișcări (figura 48). Mecanismul translațional portabil împreună cu centrul de masă C și mișcarea relativă față de axele x1, y1, z1 se deplasează împreună cu centrul de masă. Atunci viteza punctelor. Dar mișcarea portabilă este progresivă. Prin urmare, vitezele de transport ale tuturor punctelor sunt egale, egale. Prin urmare, energia cinetică va fi de asemenea
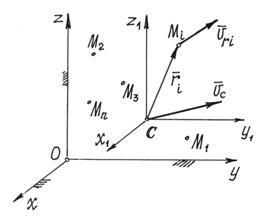
Prin definirea centrului de masă, vectorul său de rază în sistemul de mișcare (centrul de masă este la origine), și prin urmare. Derivatul timp al acestei sume este, de asemenea, zero:
Prin urmare, în final, energia cinetică a sistemului
Energia cinetică a sistemului material este suma energiei cinetice în timpul deplasării înainte cu centrul de masă și de energie cinetică în timpul deplasării acesteia în raport cu axele de coordonate, translațional se deplasează împreună cu centrul de masă.
În cazul general al mișcării unui corp, care poate fi considerată ca suma a două mișcări (mișcarea de translație este translațională împreună cu centrul de masă C și mișcarea relativă în jurul lui C), prin teorema lui Koenig (1)
unde Ix. Iy. Iz sunt principalele axe centrale ale inerției corpului.