§ 1. Curgerea vector prin suprafața închisă. Teorema Gauss.
Teorema 4.1 Dacă într-o anumită regiune a vectorului spațial coordonatele G
continuu și au derivaților continue. vectorul de curgere prin orice porțiuni închise σ suprafața netedă, dispusă în zona G, este o integrală triplă a regiunii V, delimitată de o suprafață σ:
(Formula lui Gauss) .Normal la sigma suprafața exterioară este luată.
Exemplul 4.1. Se calculează vectorul flux
printr-o suprafață închisă
x 2 + y 2 + z 2 = R 2. z = 0 (z> 0).
Decizie. În conformitate cu formula 4.1
Integrala (4.2) este convenabil calculată în coordonate sferice. avem
element de volum și
Exemplul 4.2. Se calculează fluxul vectorial peste suprafața unui torus.
Decizie. Folosind teorema Gauss, obținem că fluxul dorit P este
unde V - volumul torului. Pentru a calcula volumul V. utilizarea volumului Teorema Gulden a corpului de rotație, în virtutea cărui volum este egal cu produsul dintre piesele pătrate pe calea de rotație descris de centrul de masă al figurii în timp ce se rotește.
Să presupunem că R1 și R2 - raze interioare și exterioare ale pilier (Fig.4.1). Zona cerc S care se formează în timpul rotirii torului, este
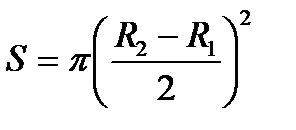
Lungimea descrisă de centrul de masă - centrul acestui cerc, - lungimea l este raza cercului. adică.
Astfel, volumul V este egal cu Torul
Z n ° σ1 k j Y i σ2 X n ° = Figura -k 4.2
Exemplul 4.3. Folosind teorema Gauss - Ostrogradskii calcula câmpul vectorial de flux
prin porțiunea exterioară suprafață laterală a z = 1 - x 2 - y 2. situat deasupra xOy avionul.
Decizie. Pentru a putea aplica teorema Gauss - Ostrogradskii, închide suprafața de jos a acestei piese XOY plan, care este limitat la un cerc
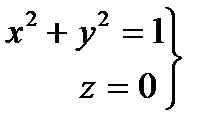
Fie v - volumul solidului rezultat delimitat de suprafața netedă σ pe porțiuni închise. constând dintr-o porțiune a unui paraboloid de revoluție σ1 z = 1 - x 2 - (. Figura 4.2) y 2 și partea σ2 planul z = 0..
Fluxul peste suprafața sigma vectorială a teoremei Gauss - este Ostrogradskii
În virtutea aditivului de curgere va avea
Prin urmare, debitul dorit
Și vector de curgere P2 prin cercul este
Deoarece planul z = 0, avem
§ 2. Divergența câmpului vectorial.
Conceptul vectorului de flux prin suprafața închisă conduce la conceptul de divergență sau câmp de divergență. Acest concept oferă o anumită caracteristică cantitativă a câmpului de la fiecare punct.
Fie M - punctul domeniului studiat. Σ înconjoară suprafața formei arbitrare, de exemplu, o sferă de rază suficient de mică. Zona delimitată de suprafața σ. lăsați-l să fie (V), și V. volumică ia în considerare atitudinea
Definiția 4.1. Dacă raportul (4.3) are o limită finită, când suprafața (V) este contractat la punctul M, atunci această limită se numește divergența câmpului vectorial (vector divergență a) la punctul M și este notat div un (M). astfel încât
Formula (4.4) oferă o definiție invariant de divergență. Această definiție înseamnă că divergența câmpului și la punctul M este densitatea în vrac și vectorul flux la acel punct.
Punctele M și câmp vectorial (M) în care div a> 0. numitele surse, precum și punctul în care div A<0 называются стоками векторного поля.
Divergența câmpului vectorial este o funcție scalară a câmpului de puncte.
Dacă coordonatele vectorului
au derivate parțiale continue în vecinătatea punctului M (x, y, z). apoi, folosind definiția invariantă a teoremei divergență de Gauss - Ostrogradskii obține că
Toate valorile din ecuația (4.5) sunt considerate în același punct M (x, y, z).
Folosind formula (4.5) pentru divergența poate teorema lui Gauss - Ostrogradskii (. Vezi § 1) să fie scrise în formă de vector,
Exemplul 4.4. Folosind invariant definit calcula divergența vectorului a = xi la punctul O (0, 0, 0), selectarea suprafețelor ca sigma din jurul punctului O. σε sfera ε rază centrată în acel punct.
Decizie. Prin definiție, divergențele în acest moment avem
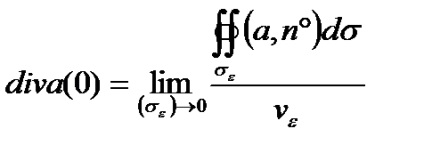
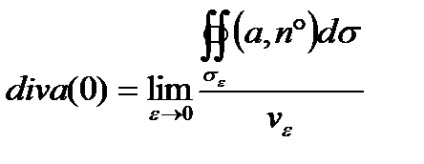
Dar, pe măsură ce volumul unei sfere este egal cu
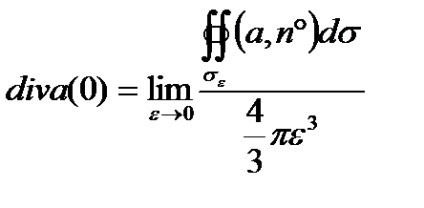
Se calculează fluxul prin sfera acestui σε vector. Vectorul normal de unitate la câmpul n ° σε care vizează raza sferei, astfel încât să puteți pune:
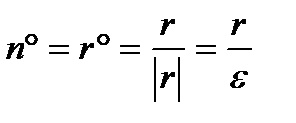
Fluxul Căutând este egal cu
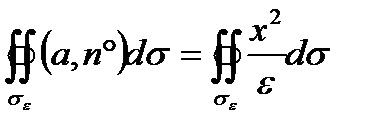
Revenind la coordonatele pe σε sferei
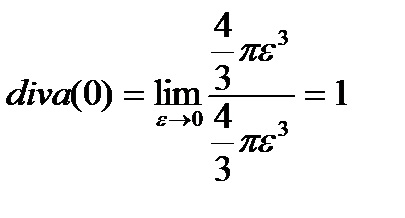
Exemplul 4.5. Calculați div r.
Decizie. Avem = xi + yj + zk, astfel încât P = x, Q = y, R = z, și, prin urmare, formula (4.5)
Exemplul 4.6. Calculați div (u, a), în cazul în care u (M) - funcția scalară, și (M) = P (x, y, z) i + Q (x, y, z) j + R (x, y, z) k - vectorială.
Decizie. Folosind formula (4.5), găsim
Exemplul 4.7. Găsiți divergența vectorului
în care: - distanța de la origine la punctul M variabilă (x, y, z).
Decizie. Folosind formula (4.7), obținem
.