Una dintre problemele de modelare econometrice este de a prezice comportamentul fenomenului studiat sau procesul în viitor. În cele mai multe cazuri, această problemă poate fi rezolvată pe baza modelelor de regresie care pot fi folosite pentru a prezice comportamentul variabilei eficiente, în funcție de comportamentul variabilelor factorului.
Să considerăm procesul de previzionare pentru modelul de regresie liniară camera de aburi.
Scoring punct peremennoyu de predicție bazată pe modelul de regresie liniară pereche pentru o anumită valoare a variabilei factor Xm este realizată prin formula:
Punctul de predicție variabilă efectivă ym cu un nivel de încredere γ, sau (1-a) se încadrează în intervalul de predicție, definită ca:
t - t-Student criteriu, care este determinat în funcție de un nivel de semnificație predeterminat, iar numărul de grade de libertate (n-2) pentru un model de regresie liniară a aburului;
ω (m) - valoarea erorii de predicție la punctul m.
Pentru modelul de regresie liniară valoarea erorii de predicție a aburului este determinată prin formula:
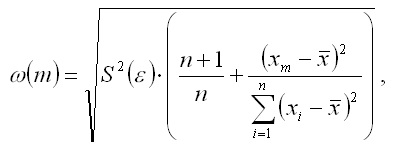
în cazul în care S2 (ε) - estimare imparțială a varianței erorii aleatoare a modelului de regresie liniară pereche.
Luați în considerare în procesul de determinare a valorii p erorii de predicție (m).
Să presupunem că, pe baza datelor eșantionului a fost construit un model de regresie liniară tipuri de cameră de aburi:
Factor x variabilă în modelul este prezentat într-o formă centrată.
Problema constă în calcularea predicția eficientă a y pentru o anumită valoare a factorului o Xm variabilă, t. E.
Așteptarea efectivă variabilă y la m se calculează cu formula:
Dispersia variabilă efectivă y la m se calculează cu formula:
unde D (β0) - dispersia parametru estimare β0 model de regresie liniară cu abur, care se calculează cu formula:
Prin urmare, estimarea punctuală pentru variabila prognoza efectiva la punctul m are o distribuție normală cu așteptări
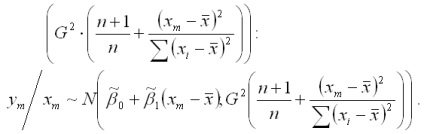
Dacă eficientă formulă de dispersie variabilă la punctul m în locul G2 dispersiei substitui selectiv evaluare S2, atunci obținem un interval de încredere pentru eficienta predicția y pentru o anumită valoare a factorului variabil xm:
în cazul în care estimarea eșantionului a varianței populației S2 pentru un model de regresie liniară a aburului se calculează cu formula:
În acest caz, intervalul de prognoză poate fi transformată în:
QED.