Lecții de focalizare
Obiective lecție
- Faceți cunoștință cu noile definiții și amintesc unele deja studiate.
- Aprofundarea cunoștințele lor de geometrie, studia povestea de origine.
- Consolidarea cunoștințelor teoretice ale studenților despre triunghiuri în practică.
- Pentru a familiariza studenții cu delta egipteană și utilizarea acesteia în construcții.
- Aflați cum să aplice proprietățile de cifre pentru a rezolva problemele.
- Educațional - să dezvolte o atenție, diligență, perseverență, gândirea logică, vorbire matematică elevilor.
- Educațional - prin tutorial pentru a educa o atitudine atentă unii față de alții, pentru a da posibilitatea de a asculta la prieteni, asistență reciprocă, auto-suficiență.
obiectivele lecției
- Verificați capacitatea elevilor de a rezolva probleme.
plan de lecție
- Observații introductive.
- Este util să ne amintim.
- Toeugolnik.
- triunghi egiptean.
remarci de deschidere

Oare vechii egipteni în matematică și geometrie? Nu numai că știa, dar, de asemenea, utilizat în mod constant în crearea de capodopere arhitecturale si chiar. la anuala de marcare a câmpurilor în care apa în timpul unei inundații pentru a distruge toate limitele. Chiar și acolo a fost un topografi special de servicii, care folosesc rapid metode geometrice ale limitelor de teren au fost reduse atunci când apa diminuat.
Nu se cunoaște modul în care ne numim generația noastră tânără care crește pe computerele, făcând posibilă nu să memoreze tabla înmulțirii și să producă în mintea celuilalt calcul matematic elementar sau construcții geometrice. Poate chelovekorobotami sau cyborgi. Grecii numit oameni care nu au putut, fără a demonstra că o teoremă simplu, profan. Prin urmare, nu este surprinzător faptul că teoria în sine, care este utilizat pe scară largă în domeniul științelor aplicate, inclusiv câmpuri pentru aspectul sau construirea de piramide, grecii antici numit „pod de măgari.“ Și ei sunt foarte bine cunoscute matematică egiptene.
Este util să ne amintim
triunghi
Triangle rectilinie, o parte a planului delimitat de trei segmente de linie (laturi ale triunghiului (în geometrie)) având pairwise la un capăt comun (noduri de triunghi (geometrie)). Triunghi în care lungimile laturilor sunt egale se numește echilateral. sau dreapta. Un triunghi cu două laturi egale - isoscel. triunghi ascutitunghic se numește. dacă toate colțurile ascuțite sale; dreptunghiular - în cazul în care unul dintre unghiurile sale este drept; obtuz - în cazul în care unul dintre unghiurile sale este obtuz. Mai mult de un mod direct sau obtuz unghi triunghi (în geometrie) nu poate avea, ca suma tuturor celor trei unghiuri egale cu două unghiuri drepte (180 ° sau, în radiani, p). Zona de triunghi (în geometrie) este ah / 2, și în care - fiecare dintre laturile triunghiurilor, luate baza sa, o h - înălțimea potrivită. Părțile laterale ale triunghiului sunt supuse condiției ca lungimea fiecăreia dintre ele este mai mică decât suma și mai mare decât diferența dintre lungimile celorlalte două laturi.
Triangle - un poligon simplu. 3 având un vârf (colț) și 3 părți; o parte a planului delimitat de trei puncte, și trei segmente în perechi de legătură aceste puncte.
- Trei puncte în spațiu, care nu se află pe o linie dreaptă corespunde unul și numai un singur plan.
- Orice poligon poate fi împărțit în triunghiuri - un proces numit triangulare.
- Există o ramură a matematicii, care este în întregime dedicat studiului de modele de triunghiuri - Trigonometrie.
tipuri de triunghiuri
Deoarece suma unghiurilor unui triunghi este de 180 °, atunci cel puțin două colțuri ale triunghiului ar trebui să fie acută (mai mic de 90 °). Următoarele tipuri de triunghiuri:
- Dacă toate unghiurile unui triunghi triunghi acut este numit ascutitunghic;
- Dacă unul dintre unghiurile unui triunghi este obtuz (mai mare de 90 °), atunci triunghiul se spune obtuz;
- Dacă unul dintre unghiurile unui triunghi linie (egal cu 90 °), atunci triunghiul este numit dreptunghiular. Cele două părți care formează un unghi drept se numesc picioare, iar partea opusă unghiului drept se numeste ipotenuza.
Prin numărul de laturi egale
- Versatil numit triunghi în care lungimea celor trei laturi sunt distincte.
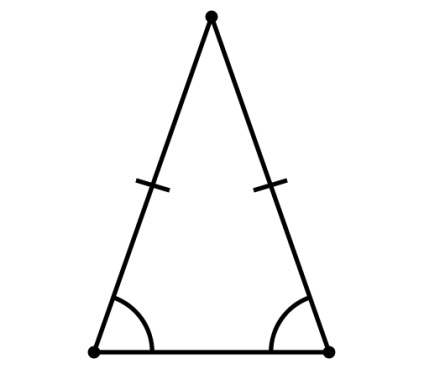
- Se numește un triunghi isoscel în care cele două părți sunt egale. Aceste partide sunt numite parte, a treia parte se numește bază. Într-un triunghi isoscel unghiurile de bază sunt egale. Înălțimea, mediană și bisectoarea unui triunghi isoscel, coborât la baza aceeași.
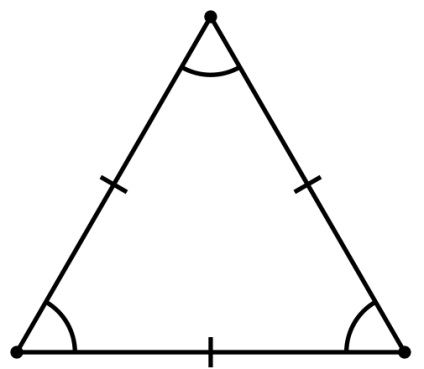
- Se numește un triunghi echilateral, în care toate cele trei laturi sunt egale. În toate colțurile unui triunghi echilateral sunt 60 °, iar centrele cercurilor inscriptionate și circumscrise coincid.


triunghi egiptean
triunghi egiptean - triunghi înclinat cu un raport de aspect de 3: 4: 5. Cantitatea numitului numere a fost utilizat (3 + 4 + 5 = 12), încă din cele mai vechi timpuri ca o unitate în construirea unghiuri drepte multiplicitate cu o frânghie, nodurile marcate de pe 3/12 și 7/12 din lungimea sa. triunghi egiptean folosit în arhitectura din Evul Mediu pentru construirea de scheme de proporționalitate.
Deci, de unde începe? Sunt aici cu: 3 + 5 = 8, iar numărul 4 este jumătate din 8. Oprire! Numerele 3, 5, 8. Nu-ele arata ca ceva foarte familiar? Desigur, ei au o relație directă cu secțiunea de aur, și introduceți așa-numitul „numărul de aur“ 1, 1, 2, 3, 5, 8, 13, 21. În această serie, fiecare număr succesiv este suma dintre ultimele două: 1 + 1 2 = 1 + 2 = 3, 3 + 2 = 5 3 + 5 = 8, și așa mai departe. Se pare că triunghiul egiptean este legat de secțiunea de aur? Și egiptenii antici știau ce trebuia să facă? Dar să nu sari la concluzii. Este necesar de a afla detalii mai precis.
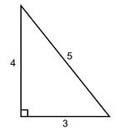
Pentru a demonstra teorema despre triunghiul egiptean necesitatea de a utiliza un segment de linie de lungime cunoscută A-A1 (Fig.). El va servi ca unitate de măsură la scară, și va determina lungimea de toate laturile triunghiului. Trei segmente A-A1 puțin egale în lungime de partea BC a triunghiului, care raportul este 3. Un segment A patru A1 egal cu lungimea a doua parte, în care raportul exprimat de numărul 4. În final, a treia lungime laterală egală cu cinci segmente A -A1. Și apoi, cum se spune, un truc. Pe hârtie, efectuam segmentul BC, care este cea mai mică latură a triunghiului. Apoi, de la B raza punctului egal cu segmentul cu un raport de 5, țineți busola cerc arc, cât și din punctul C -arc cerc de rază egală cu lungimea segmentului cu un raport de 4. Dacă acum punctul de intersecție al arcelor conecta cu liniile B și C, obținem un triunghi dreptunghiular un raport de aspect al 3. 4. 5.
QED.
triunghi egiptean folosit în arhitectura din Evul Mediu pentru construirea schemelor de proporționalitate și de a construi unghiuri drepte topografi și arhitecți. triunghi egiptean este cea mai simplă (și primul cunoscut) de triunghiuri Geronovyh - triunghiuri cu laturile intregi si patrate.
triunghi egiptean - enigma antichității
Fiecare dintre voi știe că Pitagora a fost un matematician mare, care a contribuit enorm la dezvoltarea algebră și geometrie, dar chiar și mai mult, el a câștigat faima pentru teorema lui.

Și a deschis Pitagora teorema triunghiul egiptean într-un moment în care el a vizitat în Egipt. Stau în țară, omul de știință a fost fascinat de splendoarea și frumusețea piramide. Poate că acest lucru este exact ceea ce a fost un impuls pe care l-au pus pe ideea că forma de piramidă este văzută în mod clar unele model bine definit.
Istoria descoperirii
Numele triunghiului egiptean a fost din cauza grecilor și Pitagora, care au fost vizitatori frecvente în Egipt. Sa întâmplat aproximativ VII-V-lea î.Hr.. e.
Celebre Piramida lui Keops, de fapt, este un poligon dreptunghiular, dar triunghiul egiptean sacru este considerat a fi o piramidă Kefren.
Locuitorii din natura Egipt triunghi egiptean, a scris Plutarh, au fost comparate cu vatra familiei. Aceste interpretări ar putea fi auzit că această formă geometrică a piciorului său vertical simbolizează omul, cifra de bază se referă la feminin ipotenuza de sus și piramida având în vedere rolul copilului.
Iar rezultatul studierii subiectului știți bine că raportul de aspect al această cifră este de 3: 4: 5 și, în consecință, ne conduce la teorema lui Pitagora, deoarece 32 + 42 = 52.
Iar atunci când ia în considerare faptul că la baza piramidei Kefren este triunghiul egiptean, se poate concluziona, oamenii din lumea antică știa celebra teorema mult timp înainte de a fi fost formulată de Pitagora.
Principala caracteristică triunghiul egiptean probabil a avut raportul original, care a fost prima și cea mai simplă de triunghiuri Geronovyh, ca ambele părți și au o suprafață numere întregi.
Caracteristici triunghi egiptean
Acum, să discutăm mai detaliat cu privire la caracteristicile distinctive ale triunghiului egiptean:
• În primul rând, așa cum am spus, toate laturile sale și zona este format din numere întregi;
• În al doilea rând, teorema lui Pitagora, știm că suma pătratelor picioarelor este egală cu pătratul ipotenuzei;
• În al treilea rând, cu ajutorul triunghiului, puteți măsura unghiuri în spațiu, care este foarte convenabil și necesară pentru construcția de clădiri. Și confort este ceea ce știm, că acest triunghi este un unghi drept.
• În al patrulea rând, după cum știm deja, de asemenea, că, chiar dacă nu există instrumente de măsură adecvate, acest triunghi poate fi ușor de construit folosind o frânghie simplă.
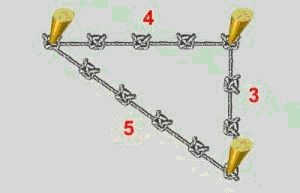
Utilizarea triunghiului egiptean
În antichitate, în arhitectura și construcția triunghiului egiptean foarte popular. El a fost necesar în special în cazul în care pentru a construi unghiul drept, folosind o frânghie sau un cablu.
Este cunoscut faptul că pentru a amâna unghiul drept în spațiu, este o sarcină destul de dificilă și, prin urmare, intreprinzatori egiptenii au inventat un mod interesant de a construi un unghi drept. În acest scop au luat coarda pe care notate neted noduli douăsprezece părți și apoi din frânghie pliat triunghi cu laturi care sunt egale cu 3. Porțiunile 4 și 5 și, ca rezultat nici o problema, da un triunghi dreptunghic. Datorită acestui instrument complicat, egiptenii cu măsură de mare precizie pe teren pentru lucrări agricole, construirea de case și piramide.
Așa o vizită în Egipt și de a studia caracteristicile unei piramide egiptene împins teorema lui Pitagora pentru deschiderea sa, care, întâmplător, a lovit Cartea Recordurilor ca teorema, care are cea mai mare cantitate de dovezi.
fapt interesant
roți triunghiulare Reuleaux
Roata - rotund (de regulă), liber de rotație sau montat pe axul de antrenare, care îi permite să pună corpul să se rostogolească, mai degrabă decât de diapozitive. Roata este frecvent utilizat într-o varietate de mecanisme și instrumente. Acesta este utilizat pe scară largă pentru transport.
Wheel reduce semnificativ costurile de energie pentru circulația mărfurilor de-a lungul suprafeței relativ plat. Când munca se realizează cu ajutorul roții împotriva forței de frecare de rulare, care în condițiile de drum artificiale este considerabil mai mică decât forța de frecare. Roțile sunt solide (de exemplu, automotoare osii montate) și constând dintr-un număr destul de mare de piese, de exemplu, în roata de vehicul include un disc, jantă, anvelopă, uneori camera, buloane și așa mai departe. uzura pneurilor auto este aproape rezolvată problema (atunci când sunt instalate unghiuri de roți). anvelopele moderne care trec peste 100 000 km. problema nerezolvata este uzura anvelopelor roților de aeronave. În contact cu roata fixă pavaj de beton pista de la o viteză de câteva sute de kilometri pe oră anvelope uzura imens.
- Ce este un triunghi?
- Tipuri de triunghiuri?
- Care este particularitatea triunghiului egiptean?
- În cazul în care triunghiul egiptean este cazul?
bibliografie
- Kuznetsov AV profesor de matematică (clasele 5-9), Kiev
- Mazur K. I. „Abordarea problemelor concurențiale cheie în matematică editat colecția MI Skanavi“
- Kobycheva Marina Viktorovna, profesor de matematică