Declarația problemei. Pentru ecuația diferențială
isoclines metodă construi o curbă integrală care trece prin punctul.
Teorema (Cauchy). Dacă funcția este continuă în punctul și în vecinătatea acesteia, există o soluție a ecuației (2), astfel încât. Dacă derivata parțială a funcției este de asemenea continuă, atunci această soluție este unică.
Problema Cauchy pentru o prima ecuație diferențială are următoarea compoziție. Pentru a găsi o soluție (integrală) a ecuației diferențiale (1) sau (2) satisface condiția inițială (). Din punct de vedere geometric, acest lucru înseamnă că printre curbele integrale ale ecuației trebuie să găsească pe cel care trece printr-un anumit punct.
Interpretarea geometrică a ecuației diferențiale (2) constă în faptul că, la fiecare punct aparținând regiunii în care toate teorema condițiile Cauchy lui, stabilește direcția liniei tangente la o singură ecuație integrală (2), care trece prin punctul, adică, direcții de teren în domeniu.
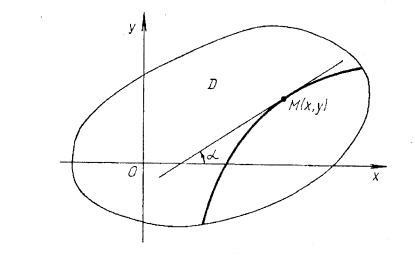
În ecuația (2) poate fi izolat de familie un parametru de curbe, fiecare dintre acestea fiind numite isocline. După cum rezultă din definiția, de-a lungul fiecărei isocline direcții de câmp în mod constant, și anume .
Găsirea isoclines și direcții de-a lungul care vă permite să organizați domeniul direcții și aproximativ construi curbele integrale ale ecuației diferențiale, adică integra grafic această ecuație.
Sarcina 8. Pentru o metodă ecuație diferențială dată isoclines construi o curbă integrală care trece prin punctul.
.
Scriem ecuația în forma:
.
Construim câmpul de direcție pentru ecuația diferențială. Isoclines zone corespunzătoare de câmp cu pantă egală sau au, adică drepte.
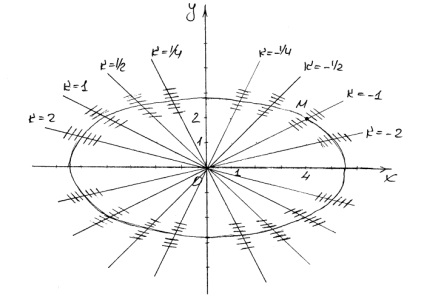
Curba integrală, evident, are o formă eliptică.